|
|
\({x^2} - 3x - 4 \le 0 \Leftrightarrow - 1 \le x \le 4\)
Trước
hết ta tìm hệ đã cho vô nghiệm \( \Leftrightarrow f\left( x \right) =
{x^3} - 3x|x| - {m^2} - 15m < 0\,\forall x \in \left[ { - 1,\,4}
\right]\)
Ta có \(f\left( x \right) = \left\{ \begin{array}{l}
{x^3} - 3{x^2} - {m^2} - 15m\,,\,0 \le x \le 4\\
{x^3} + 3{x^2} - {m^2} - 15m\,,\, - 1 \le x \le 0
\end{array} \right. \Rightarrow f'\left( x \right) = \left\{ \begin{array}{l}
3{x^2} - 6x\,,\,0 < x < 4\\
3{x^2} + 6x\,,\, - 1 < x < 0
\end{array} \right.\)
Do đó ta có bảng biến thiên như hình vẽ
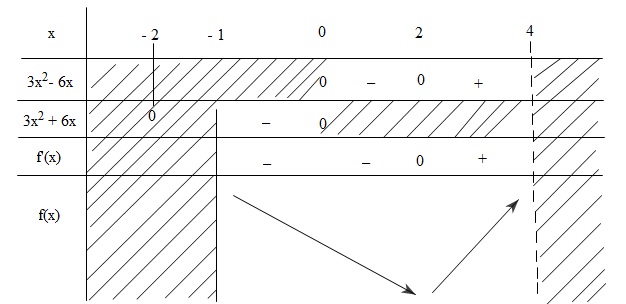
Do \(f\left( { - 1} \right) = - {m^2} - 15m + 2\,;\,f\left( 4 \right) = - {m^2} - 15m + 16\)
Suy ra \(\mathop \max \limits_{ - 1 \le x \le 4} f\left( x \right) = f\left( 4 \right) = - {m^2} - 15m + 16\)
Do đó \(f\left( x \right) < 0,\,\forall x \in \left[ {1,\, - 4} \right]\)
\( \Leftrightarrow \mathop \max \limits_{ - 1 \le x \le 4} f\left( x \right) < 0 \Leftrightarrow {m^2} + 15m - 16 > 0 \)
Như vậy để hệ PT ban đầu có nghiệm \(\Leftrightarrow{m^2} + 15m - 16 \le 0\Leftrightarrow - 16 \le m \le 1 \)
|
|
|
Trả lời 20-07-12 02:51 PM
|
|