|
|
Bài toán này có một lời giải khá gọn bằng công thức Heron và BĐT Cauchy, mình sẽ thử giải bằng hình phẳng :D
Giả sử $\Delta ABC$ có chu vi không đổi và $AB<AC$. Trên 2 tia $AB$ và $AC$ chọn 2 điểm $B',C'$ sao cho $AB'+AC'=AB+AC$. Ta sẽ chứng minh $\Delta AB'C'$ có diện tích lớn hơn $\Delta ABC$ nhưng có chu vi nhỏ hơn.
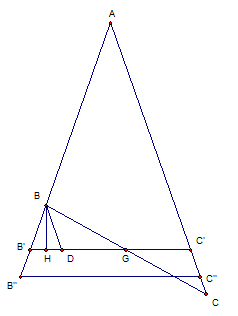
Dễ thấy $B'$ nằm ngoài cạnh $AB$ và $C'$ nằm trong cạnh $AC$. Chọn $D$ trên $B'C'$ sao cho $BD//AC$. Gọi $G=BC\times B'C'$. Dễ thấy $\Delta BDG=\Delta CC'G$. Do đó:
$S_{ABC}=S_{ABGC}+S_{CC'G}=S_{ABCD}+S_{BDG}=S_{ABDC'}<S_{AB'C'}.$
Đồng thời: $BC=2BG>2GH=B'C' \Rightarrow AB+BC+CA>AB'+B'C'+C'A$.
Khi đó chỉ cần chọn $B''$ và $C''$ trên $AB$ và $AC$ sao cho $\frac{AB''}{AB'}=\frac{AC''}{AC'}=\frac{AB+BC+CA}{AB'+B'C'+C'A}$ thì ta được $\Delta AB''C''$ có chu vi bằng chu vi $\Delta ABC$ nhưng có diện tích lớn hơn.
Tóm lại, để $\Delta ABC$ lớn nhất thì $\Delta ABC$ cân.
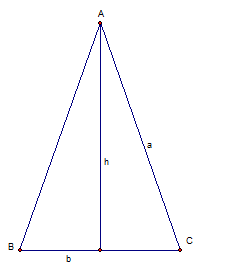
Ta xét TH $\Delta ABC$ cân tại $A$ và đặt $AB=AC=a,BC=b$ thì $2a+b=p$ không đổi.
Ta có $h^2=a^2-\frac{b^2}{4}=\frac{1}{4}p(2a-b).$ Khi đó: $S_{ABC}=\frac{1}{2}bh=\frac{1}{4}b\sqrt{p(2a-b)} $.
Theo BĐT Cauchy: $b^2(2a-b)\leq \left( \frac{2a+b}{3}\right) ^3=\frac{p^3}{27} \Rightarrow S_{ABC}\leq \frac{p^2\sqrt{3}}{36}$.
Dâus $=$ xảy ra khi và chỉ khi $b=2a-b$ hay $a=b$.
Vậy $\Delta ABC$ có chu vi không đổi sẽ có diện tích lớn nhất khi và chỉ khi $\Delta ABC$ đều.
|