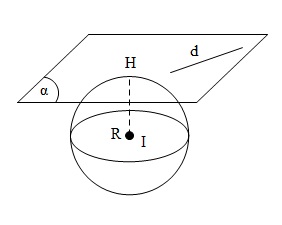
Vì mặt phẳng $(\alpha )$ chứa $d$ nên $(\alpha )$ thuộc chùm mặt phẳng có dạng
$m(8x-11y+8z-30)+n(x-y-2z)=0(m^2+n^2\neq 0)$
$\Leftrightarrow (8m+n)x+(-11m-n)y+(8mm-2n)z-30m=0 (\alpha )$
Mặt cầu $(S)$ có tâm $I(-1;3;-2), R=\sqrt{1+9+4+15}=\sqrt{29} $
Vì $(\alpha )$ tiếp xúc với mặt cầu $(S)\Leftrightarrow d(I(\alpha ))=R$
$\Leftrightarrow \frac{|-8m-n-33m-3n-16m+4n-30m|}{\sqrt{(8m+n)^2+(-11m-n)^2+(8m-2n)^2} } =\sqrt{29} $
$\Leftrightarrow |-87|=\sqrt{29}.\sqrt{249m^2+6n^2+6mn} $
$\Leftrightarrow (87)^2=29(249m^2+6mn+6n^2)$
$\Leftrightarrow 261m^2=249m^2+6mn+6n^2$
$\Leftrightarrow 12m^2-6mn-6n^2=0\Leftrightarrow 2m^2-mn-n^2=0$
Chọn $\left\{ \begin{array}{l} n=1\\ 2m^2-m-1=0\Leftrightarrow m=1, m=-\frac{1}{2} \end{array} \right. $
$\Leftrightarrow
\left\{ \begin{array}{l} m=1\\ n=1 \end{array} \right. $ hoặc $\left\{
\begin{array}{l} m=-\frac{1}{2} \\ n=1 \end{array} \right. $
$m=1$ và $n=1:(\alpha ):9x-12y+6z-30=0\Leftrightarrow 3x-4y+2z-10=0 (\alpha_1 )$
$m=-\frac{1}{2} $ và $n=1:(\alpha ):-3x+\frac{9}{2}y-6z+15=0 $
$\Rightarrow -6x+9y-12z+30=0\Leftrightarrow 2x-3y+4z-10=0 (\alpha_2 )$
Vậy có hai phương trình mặt phẳng $(\alpha )$ thỏa mãn yêu cầu bài toán:
$(\alpha_1 ):3x-4y+2z-10=0; (\alpha_2 ):2x-3y+4z-10=0$