|
|
giải đáp
|
Hình chóp $S.ABCD$
|
|
|
|
a) Gọi $SG_1, SG_2$ cắt $BC,AD$ tại $R, F$ thì $R,F$ là trung điểm của $BC,AD$.
Ta có
$SG_1 : SR = SG_2 : SF =2 : 3 \Rightarrow G_1G_2 \parallel RF \parallel AB \parallel CD \Rightarrow $ đpcm.
|
|
|
|
giải đáp
|
Hình chóp.
|
|
|
|
Vì $G_1, G_2$ là các trọng tâm nên ta có
$CG_1 : CM = CG_2 : CP =2:3 \Rightarrow G_1G_2 \parallel MP \Rightarrow G_1G_2 \parallel SB \Rightarrow G_1G_2 \parallel (SBC)$
|
|
|
|
giải đáp
|
Tứ diện $ABCD$.
|
|
|
|
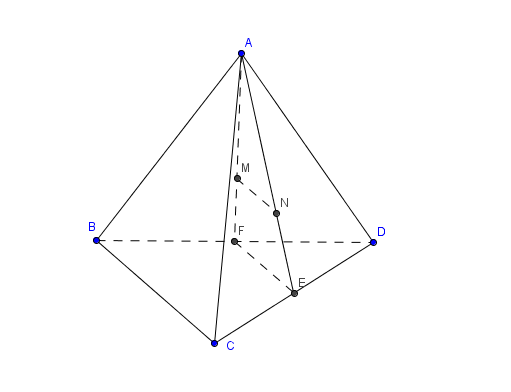 $MN \parallel EF \Rightarrow \begin{cases}MN \parallel (ABC) \\ MN \parallel (BCD) \end{cases}$ |
|
|
|
giải đáp
|
Tứ diện.
|
|
|
|
Gọi $J$ là trung điểm $AD$. Do $G$ là trọng tâm của $\triangle ABD$ nên $BG=2BJ$.
Mà $BI=2IC$ nên $IG \parallel CJ \Rightarrow IG \parallel (ACD)$
|
|
|
|
giải đáp
|
giải pt
|
|
|
|
Bằng phương pháp đồ thị ta thấy rằng PT trên chỉ có ba nghiệm. Kiểm tra rằng $f(0)=0, f(0,5)f(1) <0, f(-0,5)f(-1) <0$ như vậy có ba nghiệm thỏa mãn $x_1=0, x_2 \in (0,5;1), x_3 \in (-1;-0,5)$ 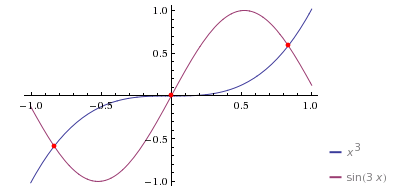 |
|
|
|
giải đáp
|
Tích phân 12
|
|
|
|
b) Ta có
$ \frac{\sin2x}{\sin^{2}x + 2\cos^{2}x}= \frac{\sin2x}{1+\cos^{2}x}= -\frac{(1+\cos^2x)'}{1+\cos^{2}x}$
Suy ra
$\int\limits_{0}^{\pi/4} \frac{\sin2x}{1+\cos^{2}x}dx=\int\limits_{0}^{\pi/4} -\frac{(1+\cos^2x)'}{1+\cos^{2}x}dx=\left[ {-\ln(1+\cos^{2}x)} \right]_{0}^{\pi/4}=\ln\frac{4}{3}$
|
|
|
|
giải đáp
|
tích phân 8
|
|
|
|
a)
$I=\int\limits_{-\pi}^{\pi}\sin mx\sin nxdx$
$=\int\limits_{-\pi}^{\pi} \frac{1}{2}(-\cos(m+n)x+\cos(m-n)x)dx$
+ Nếu $m=n$
$I=\int\limits_{-\pi}^{\pi} \frac{1}{2}(-\cos2mx+1)dx=\left[ {- \frac{1}{4}\sin2mx+\frac{1}{2}x} \right]_{-\pi}^{\pi}=\pi$
+ Nếu $m=-n$
$I=\int\limits_{-\pi}^{\pi} \frac{1}{2}(\cos2mx-1)dx=\left[ { \frac{1}{4}\cos2mx-\frac{1}{2}x} \right]_{-\pi}^{\pi}=-\pi$
+ Nếu $m\ne \pm n$
$I=\frac{1}{2}(\frac{-\sin(m+n)x}{m+n}+\frac{\sin(m-n)x}{m-n})dx\left|\begin{array}{l}\pi\\-\pi\end{array}\right.=\frac{\sin(m+n)\pi}{m+n}+\frac{\sin(m-n)\pi}{m-n}$
|
|
|
|
giải đáp
|
Tích phân 1
|
|
|
|
Ta có
$\dfrac{\cos x \ln(\sin x)}{\sin^{2}x}=-\dfrac{\cos x -\cos x( \ln(\sin x)+1)}{\sin^{2}x}=-\dfrac{\sin x.( \ln(\sin x)+1)' -(\sin x)'( \ln(\sin x)+1)}{\sin^{2}x}$
suy ra
$ \int\limits_{\pi/4}^{\pi/2} \dfrac{\cos x.\ln(\sin x)dx}{\sin^{2}x} =\left[ {-\dfrac{ \ln(\sin x)+1}{\sin x}} \right]_{\pi/4}^{\pi/2}=-1-\dfrac{\ln 2-2}{\sqrt 2}$
|
|
|
|
giải đáp
|
Tích phân 11
|
|
|
|
b) Ta có
$\int\limits_{0}^{\pi/2}\frac{\sin 2x }{4-\cos ^{2}x}dx=\int\limits_{0}^{\pi/2}\frac{-2\sin 2x }{\cos 2x -7}dx=\int\limits_{0}^{\pi/2}\frac{(\cos 2x-7)'}{\cos 2x -7}dx=\left[ {\ln|\cos 2x -7|} \right]_{0}^{\pi/2}= \ln\dfrac{4}{3} $
|
|
|
|
giải đáp
|
tích phân 10
|
|
|
|
a)
$\dfrac{1}{\tan x+1}=\dfrac{\cos x}{\sin x +\cos x}=\dfrac{1}{2}+\dfrac{1}{2}.\dfrac{\cos x-\sin x}{\sin x +\cos x}=\dfrac{1}{2}(x)'+ \dfrac{1}{2}(\ln |\sin x+ \cos x|)'$
suy ra
$\int\limits_{0}^{\pi/4}\dfrac{1}{\tan x+1}dx=\dfrac{1}{2}\left[ {x+\ln |\sin x+ \cos x|} \right]_{0}^{\pi/4}=\dfrac{\pi+\ln 4}{8}$
|
|
|
|
giải đáp
|
tích phân 10
|
|
|
|
b)
$ \int \tan^4x dx = \int(\frac{1}{\cos^2 x}\tan^2 x - \tan^2 x)
dx = \frac{\tan^3 x}{3} + \int \frac{\cos^2 x - 1}{\cos^2 x} dx=
\frac{\tan^3 x}{3} + x - \tan x +C$
Suy ra
$ \int\limits_{\pi/4}^{\pi/3} \tan^{4}xdx=\left[ {
\frac{\tan^3 x}{3} + x - \tan x } \right]_{\pi/4}^{\pi/3}=\dfrac{\pi+8}{12}$
|
|
|
|
|
|
giải đáp
|
tích phân 7
|
|
|
|
b)
$I=\int\limits_{-\pi}^{\pi}\cos mx\cos nxdx$
$=\int\limits_{-\pi}^{\pi} \frac{1}{2}(\cos(m+n)x+\cos(m-n)x)dx$
+ Nếu $m=n$
$I=\int\limits_{-\pi}^{\pi} \frac{1}{2}(\cos2mx+1)dx=\left[ { \frac{1}{4}\sin2mx+\frac{1}{2}x} \right]_{-\pi}^{\pi}=\pi$
+ Nếu $m=-n$
$I=\int\limits_{-\pi}^{\pi} \frac{1}{2}(\cos2mx+1)dx=\left[ { \frac{1}{4}\sin2mx+\frac{1}{2}x} \right]_{-\pi}^{\pi}=\pi$
+ Nếu $m\ne \pm n$
$I=\frac{1}{2}(\frac{\sin(m+n)x}{m+n}+\frac{\sin(m-n)x}{m-n})dx\left|\begin{array}{l}\pi\\-\pi\end{array}\right.=\frac{\sin(m+n)\pi}{m+n}+\frac{\sin(m-n)\pi}{m-n}$
|
|
|
|
giải đáp
|
tích phân 7
|
|
|
|
a) $ \int\limits_{0}^{\pi/2} (2\sin x+3)\cos xdx= \int\limits_{0}^{\pi/2} 2\sin x cos xdx+ 3\int\limits_{0}^{\pi/2}\cos xdx$
$=\left[ {\sin^2 x +3\sin x} \right]_{0}^{\pi/2}=4$
|
|
|
|
giải đáp
|
tích phân 6
|
|
|
|
b) Ta có
$2\sin6x.\sin2x=\cos 4x -\cos 8x$
Suy ra
$ \int\limits_{0}^{\pi/6} (\sin6x.\sin2x-6)dx= \left[ {-6x +\dfrac{1}{8}\sin 4x -\dfrac{1}{16}\sin 8x} \right]_{0}^{\pi/6}=\dfrac{3\sqrt 3}{32}-\pi$
|
|