|
|
bình luận
|
Nguyên hàm của hàm lượng giác
Hãy ấn chữ V dưới chữ đáp án để chấp nhận nếu như bạn thấy lời giải này chính xác, và nút mũi tên màu xanh để vote up nhé. Các bài tiếp theo mình sẽ sẵn sàng giúp đỡ bạn.
|
|
|
|
|
|
|
|
giải đáp
|
Nguyên hàm của hàm lượng giác
|
|
|
|
4. Xét : $F(x)=\int\limits \frac{\sin x}{1+\sin
2x}dx=\frac{1}{2}\int\limits \frac{(\sin x+\cos x)-(\cos x-\sin
x)}{(\sin x+\cos x)^2}dx $
$=\frac{1}{2}\int\limits \frac{dx}{\sin x+\cos x}-\frac{1}{2}\int\limits \frac{(\cos x-\sin x)dx}{(\sin x+\cos x)^2} $
Tính
: $I_1= \frac{1}{2}\int\limits \frac{dx}{\sin x+\cos x} $.Đặt $t=\tan
\frac{x}{2} \Rightarrow dx=\frac{2dt}{1+t^2}; \sin x+\cos
x=\frac{-t^2+2t+1}{1+t^2} $
Lúc đó : $I_1 =\frac{1}{2}\int\limits
\frac{2dt}{-t^2+2t+1}=\frac{1}{4 {\sqrt{2}} }\int\limits (\frac{1}{t-1-
{\sqrt{2}} }- \frac{1}{t-1+ {\sqrt{2}} } )dt $
$ \Rightarrow {I_1}
= \frac{1}{{4\sqrt 2 }}\ln \left| {\frac{{t - 1 - \sqrt 2 }}{{t - 1 +
\sqrt 2 }}} \right| + {C_1} = \frac{1}{{4\sqrt 2 }}\ln \left|
{\frac{{\tan \frac{x}{2} - 1 - \sqrt 2 }}{{\tan \frac{x}{2} - 1 + \sqrt 2
}}} \right| + {C_1}\,\,(1)$
Tính : $I_2=\frac{1}{2}\int\limits
\frac{(\cos x-\sin x)dx}{(\sin+\cos x)^2}=\frac{1}{2} \int\limits
\frac{d(\cos x+\sin x)}{(\cos x+\sin x)^2}=-\frac{1}{2}\frac{1}{\sin
x+\cos x}+C_2 (2) $
Từ $(1) và (2) $ :
$F(x)=
\frac{1}{{4\sqrt 2 }}\ln \left| {\frac{{\tan \frac{x}{2} - 1 - \sqrt 2
}}{{\tan \frac{x}{2} - 1 + \sqrt 2 }}} \right|+\frac{1}{2}\frac{1}{\sin
x+\cos x}+ C $
Trong đó $C=C_1-C_2 :$ là hằng số tùy ý
|
|
|
|
sửa đổi
|
Nguyên hàm của hàm lượng giác
|
|
|
|
Nguyên hàm của hàm lượng giác 1. $\int\limits _ \frac{cosx}{\sqrt{1+4sinx}}dx$2. $\int\limits _ sin^{6}x.sin2xdx$ 3. $\int\limits _ \frac{dx}{sin^{3}xcos^{5}x}$4. $\int\limits _ \frac{sinx}{1+sin2x}dx$
Nguyên hàm của hàm lượng giác 1. $\int\limits\frac{ \cos x}{\sqrt{1+4 \sin x}}dx$2. $\int\limits \sin^{6}x. \sin2xdx$ 3. $\int\limits \frac{dx}{ \sin^{3}x \cos^{5}x}$4. $\int\limits\frac{ \sin x}{1+ \sin2x}dx$
|
|
|
|
bình luận
|
Phương trình và bất phương trình.
Hãy ấn chữ V dưới đáp án để chấp nhận nếu như bạn thấy lời giải này chính xác, và nút mũi tên màu xanh để vote up nhé. Thanks!
|
|
|
|
|
|
|
|
giải đáp
|
Phương trình và bất phương trình.
|
|
|
|
3. TXĐ: $\left\{ \begin{array}{l}
1 - 4{x^2} \ge 0\\
x \ne 0
\end{array} \right.$
$ \bullet - \frac{1}{2} \le x < 0 \Rightarrow 1 - 4{x^2} < 0$ $ \Rightarrow 1 - \sqrt {1 - 4{x^2}} > 0 \Rightarrow \frac{{1 - \sqrt {1 - 4{x^2}} }}{x} < 0 (1)$ đúng $\bullet 0 < x \le \frac{1}{3} \Rightarrow 1 - 3x < 0 \Leftrightarrow (1)$ đúng $\bullet \frac{1}{3} < x \le \frac{1}{2} \Rightarrow 1 - 3x > 0$ $\begin{array}{l}
(1) \Leftrightarrow {(1 - 3x)^2} < 1 - 4{x^2} \Leftrightarrow 13{x^2} - 6x < 0\\
\Leftrightarrow 13x\left( {x - \frac{6}{{13}}} \right) < 0\forall x \in (\frac{1}{3};\frac{1}{2}{\rm{]}}
\end{array}$
Vậy ($1$) đúng $\forall x \in [ - \frac{1}{2};0{\rm{)}}\bigcup$ $(0;\frac{1}{2}{\rm{]}}$ |
|
|
|
bình luận
|
Mong mọi người giúp mình
Hãy ấn chữ V dưới chữ đáp án để chấp nhận nếu như bạn thấy lời giải này chính xác, và nút mũi tên màu xanh để vote up nhé. Các bài tiếp theo mình sẽ sẵn sàng giúp đỡ bạn.
|
|
|
|
|
|
|
|
giải đáp
|
Mong mọi người giúp mình
|
|
|
|
2. 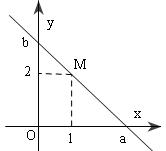 Vì $d$ cắt $(Ox), (Oy)$ nên phương trình $d$ có dạng : $\frac{x}{a} +\frac{y}{b} =1$ $d$ qua $M(1,2) : \frac{1}{a}+\frac{2}{b} =1 (*)$ Trường hợp một : $a=b\neq 0$ $(*)\Rightarrow \frac{1}{b}+\frac{2}{b}=1\Leftrightarrow b=3=a $ $\Rightarrow d : \frac{x}{3}+\frac{y}{3}=1 $ hay $x+y-3=0$ Trường hợp hai : $a=-b\neq 0$ $(*)\Rightarrow \frac{1}{-b}+\frac{2}{b}=1\Rightarrow b=1; a=-1 $ $\Rightarrow d : \frac{x}{-1}+\frac{y}{1}=1 $ hay $x-y+1=0$ Trường hợp $3: d$ qua $O(0,0),M(1,2)$ $d\equiv OM : \frac{y-y}{y_M-y_0}=\frac{x-x_0}{x_M-x_0} $ $\Rightarrow d : \frac{y}{2} =\frac{x}{1} $ hay $y=2x$ hay $2x-y=0$ |
|
|
|
bình luận
|
Giúp với!!!!!!!!!!
Hãy ấn chữ V dưới chữ đáp án để chấp nhận nếu như bạn thấy lời giải này chính xác, và nút mũi tên màu xanh để vote up nhé. Các bài tiếp theo mình sẽ sẵn sàng giúp đỡ bạn.
|
|
|
|
|
|
|
|
giải đáp
|
Giúp với!!!!!!!!!!
|
|
|
|
Lời giải này có yêu cầu trả vỏ sò để xem. Bạn hãy link trên để vào xem chi tiết
|
|
|
|
|
|
bình luận
|
mọi người giúp với
Hãy ấn chữ V dưới đáp án để chấp nhận nếu như bạn thấy lời giải này chính xác, và nút mũi tên màu xanh để vote up nhé. Thanks!
|
|
|
|
|
|
|
|
giải đáp
|
mọi người giúp với
|
|
|
|
a. $|2\sin n + 3\cos n| \le 2|\sin n|+3|\cos n|=5$. Suy ra $-\frac{5}{n^2+1} \le \frac{2\sin n + 3\cos n}{n^2+1} \le \frac{5}{n^2+1}$. Mặt khác $\lim \frac{5}{n^2+1} = \lim\left ( - \frac{5}{n^2+1} \right )=0\Rightarrow \lim \frac{2\sin n + 3\cos n}{n^2+1}=0.$ |
|
|
|
|
|
|
|
bình luận
|
cấp số nhân
Hãy ấn chữ V dưới đáp án để chấp nhận nếu như bạn thấy lời giải này chính xác, và nút mũi tên màu xanh để vote up nhé. Thanks!
|
|
|
|
|
|