|
|
giải đáp
|
help me
|
|
|
|
Theo giả thiết: $\frac{1}{xy}+\frac{1}{yz}+\frac{1}{zx}=1$
Ta có:
$P=\frac{(x-1)+(y-1)}{x^2}+\frac{(y-1)+(z-1)}{y^2}+\frac{(z-1)+(x-z)}{z^2}-(\frac{1}{x}+\frac{1}{y}+\frac{1}{z})$
$=(x-1)(\frac{1}{x^2}+\frac{1}{z^2})+(y-1)(\frac{1}{x^2}+\frac{1}{y^2})+(z-1)(\frac{1}{y^2}+\frac{1}{z^2})-(\frac{1}{x}+\frac{1}{y}+\frac{1}{z})$
$\geq \frac{2(x-1)}{xz}+\frac{2(y-1)}{xy}+\frac{2(z-1)}{yz}-(\frac{1}{x}+\frac{1}{y}+\frac{1}{z})$
$=\frac{1}{x}+\frac{1}{y}+\frac{1}{z}-2(\frac{1}{xz}+\frac{1}{xy}+\frac{1}{yz})=\frac{1}{x}+\frac{1}{y}+\frac{1}{z}-2 (1)$
Mà $(\frac{1}{x}+\frac{1}{y}+\frac{1}{z})^2 \geq 3(\frac{1}{xz}+\frac{1}{xy}+\frac{1}{yz})=3 (2)$
Từ $(1)$ và $(2) \Rightarrow P \geq \sqrt{3}-2$
Kết luận: Vậy $\min P=\sqrt{3}-2 \Leftrightarrow x=y=\sqrt{3}$
|
|
|
|
được thưởng
|
Đăng nhập hàng ngày 05/02/2014
|
|
|
|
|
|
|
|
|
|
được thưởng
|
Đăng nhập hàng ngày 30/01/2014
|
|
|
|
|
|
|
|
|
|
bình luận
|
Giúp với!!!
Hãy ấn chữ V dưới chữ đáp án để chấp nhận nếu như bạn thấy lời giải này chính xác, và nút mũi tên màu xanh để vote up nhé. Các bài tiếp theo mình sẽ sẵn sàng giúp đỡ bạn.
|
|
|
|
|
|
|
|
giải đáp
|
Giúp với!!!
|
|
|
|
Hiển nhiên thấy $c$ và $d$ có thể chéo nhau (bao gồm cả song song, vuông góc), cắt nhau nhưng không thể trùng nhau.
|
|
|
|
bình luận
|
những bài tập này khó wa ! giúp mình nhé !
Hãy ấn chữ V dưới chữ đáp án để chấp nhận nếu như bạn thấy lời giải này chính xác, và nút mũi tên màu xanh để vote up nhé. Các bài tiếp theo mình sẽ sẵn sàng giúp đỡ bạn.
|
|
|
|
|
|
|
|
giải đáp
|
những bài tập này khó wa ! giúp mình nhé !
|
|
|
|
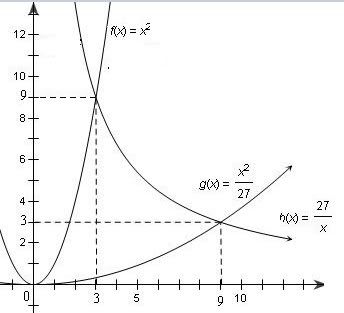 Xét các PT giao điểm : Xét các PT giao điểm :
$x^2=\frac{x^2}{27}\Leftrightarrow x=0$
$x^2=\frac{27}{x}\Leftrightarrow x=3$
$\frac{x^2}{27}=\frac{27}{x}\Leftrightarrow x=9$ $S=\int\limits_{0}^{3}(x^2-\frac{x^2}{27} ) dx+\int\limits_{3}^{9} (\frac{27}{x} -\frac{x^2}{27} )$ $=\frac{26}{27}
.\frac{x^3}{3} \mathop |\nolimits_0^3 +27\ln x\mathop |\nolimits_3^9
-\frac{1}{27} .\frac{x^3}{3} \mathop |\nolimits_3^9 =27\ln3$ (đvdt) |
|
|
|
|
|
được thưởng
|
Đăng nhập hàng ngày 24/01/2014
|
|
|
|
|
|
|
|
được thưởng
|
Đăng nhập hàng ngày 23/01/2014
|
|
|
|
|
|
|
|
bình luận
|
Hình khó
Em xem lại kỹ nhé! Anh không hề nhắc đến những thứ em vừa viết trong bài giải. A chỉ đưa ra bổ đề và áp dụng của nó để giải bài toán. Nếu chính em cần thì chính xác là $MO'' = \frac12 EO'$.
|
|
|
|
|
|
|
|
bình luận
|
Bất đẳng thức.
Hãy ấn chữ V dưới chữ đáp án để chấp nhận nếu như bạn thấy lời giải này chính xác, và nút mũi tên màu xanh để vote up nhé. Các bài tiếp theo mình sẽ sẵn sàng giúp đỡ bạn.
|
|
|
|
|
|
|
|
bình luận
|
Tính giới hạn ?????
Hãy ấn chữ V dưới chữ đáp án để chấp nhận nếu như bạn thấy lời giải này chính xác, và nút mũi tên màu xanh để vote up nhé. Các bài tiếp theo mình sẽ sẵn sàng giúp đỡ bạn.
|
|
|
|
|
|