b/ EN và CQ lần lượt là đường cao trong tam giác đều EAD và CAB
=> EN vuông góc với AD, CQ vuông góc với AB
=> EN//CQ
=> CNEQ là hình thang (đpcm) 

a/ $\Delta$AED là tam giác cân do AD= AE
Mà $\widehat{DAE}=\widehat{BAC}= 60^{0}$ 
=> AED là tam giác đều 
=> $\widehat{ADE}=60^{0}=\widehat{ABC}$  
=> DE//BC
=> BCDE là hình thang (1) 
Mặt khác: $\Delta$EAB= $\Delta$DAC (c.g.c)
=> EB=DC (2)
(1)(2)=> BCDE là hình thang cân 

e/ gọi G, N, I lần lượt là trung điểm của AC', BC, A'D'
Có BA'// NI  => góc giữa AC' và BA' là góc giữa AC' và NI chính là góc NGC'
Có $AC'^{2}= AA'^{2}+A'C'^{2}$=> AC'= a$\sqrt{3}$ => GC' = $\frac{a\sqrt{3}}{2}$
Có $NC'^{2}=NC^{2}+CC'^{2}$=> NC'= $\frac{a\sqrt{5}}{2}$
Có: NG= 1/2 NI= 1/2 BA'= $\frac{a\sqrt{2}}{2}$
Ta thấy: $NG^{2}+GC'^{2}=NC'^{2}$
 => $\Delta$NGC' là tam giác vuông tại G => $\widehat{NGC'}$= $90^{0}$
Vậy góc giữa AC' và BA' bằng  $90^{0}$

d/  AB'// DC'
=> góc giữa AB' và BC' là góc giữa DC' và BC', là $\widehat{DC'B}$ 
$\Delta$ DC'B có DC'=C'B=BD= a$\sqrt{2}$
=> DC'B là tam giác đều => $\widehat{DC'B }= 60^{0}$ 

c/  B'C// A'D
=> góc giữa B'C và A'C' là góc giữa A'D và A'C', là $\widehat{DA'C'}$ 
$\Delta$ DA'C' có DA'=A'C'=C'D= a$\sqrt{2}$
=> DA'C'' là tam giác đều => $\widehat{DA'C' }= 60^{0}$ 

b/ AB vuông góc với BC và BB' => AB vuông góc với (BCC'B')
=> AB vuông góc với B'C' => góc giữa AB và B'C' bằng $90^{0}$ 

a/ BA'// CD'
=> góc giữa AC và BA' là góc giữa AC và CD', là $\widehat{ACD'}$ 
$\Delta$ ACD' có AC=CD'=AD'= a$\sqrt{2}$
=> ACD' là tam giác đều => $\widehat{ACD' }= 60^{0}$ 

Lời giải này có yêu cầu trả vỏ sò để xem. Bạn hãy link trên để vào xem chi tiết

b/ Cách khác:
Có $SB^{2}= SA^{2}+AB^{2}$=> SB= a$\sqrt{3}$
Mà SE= SB/3 => SE=  a$\sqrt{3}$/3
Xét $\Delta$SAE: cosASE= SE/SA= $\frac{\sqrt{3}}{3}$ 
sinSAE= SE/AS=  $\frac{\sqrt{3}}{3}$ 
=>  cosASE= sinSAE
=> $\widehat{ASE} và\widehat{SAE}$  là 2 góc phụ nhau => $\widehat{ASE} +\widehat{SAE}$  = $90^{0}$
=> $\widehat{SEA}$=  $90^{0}$
=> SB vuông góc với AE
Mặt khác SB vuông góc với AD (do AD vuông góc với mp(SAB))
=> SB vuông góc với (AED) (ĐPCM) 

Cách khác:

a/ Ta di chứng minh: DM vuông góc với AC
Gọi O là giao của DM và AC
Có tan ACB= a$\sqrt{2}$/a= $\sqrt{2}$
tan DMA= $\frac{a}{\frac{a\sqrt{2}}{2}}$= $\sqrt{2}$
=> $\widehat{ACB}$= $\widehat{DMA}$ hay  $\widehat{ACB}$= $\widehat{AMO}$
=> $\Delta$AMO $\sim$$\Delta$ACB => $\widehat{AOM}$= $\widehat{ABC}$ =$90^{0}$
=> DM vuông góc với AC
Mặt khác AC lại vuông góc với SA => DM vuông góc với (SAC) 

Số cách sắp xêp chỗ cho 13 em là 13!
Số các cách không thỏa mãn là:
+ 2 em nữ đứng cạnh nhau: $C^{2}_{5}. C^{4}_{9}. 4!. 2!$ 
+ 3 em nữ đứng cạnh nhau: $C^{3}_{5}. C^{3}_{9}. 3!. 3!$ 
+ 4 em nữ đứng cạnh nhau: $C^{4}_{5}. C^{2}_{9}. 2!. 4!$ 
+ 5 em nữ đứng cạnh nhau: $C^{5}_{5}. C^{1}_{9}. 1!. 5!$  
=> Số cách sắp xếp thỏa mãn là: 13!-  $C^{2}_{5}. C^{4}_{9}. 4!. 2!$ -$C^{3}_{5}. C^{3}_{9}. 3!. 3!$ -$C^{4}_{5}. C^{2}_{9}. 2!. 4!$ - $C^{5}_{5}. C^{1}_{9}. 1!. 5!$  
Vậy xác suất để không có em nữ nào đứng cạnh nhau là: P=  $\frac{13!-  C^{2}_{5}. C^{4}_{9}. 4!. 2! -C^{3}_{5}. C^{3}_{9}. 3!. 3!-C^{4}_{5}. C^{2}_{9}. 2!. 4! - C^{5}_{5}. C^{1}_{9}. 1!. 5! }{13!}$

d/ Có $\Delta$SHA= $\Delta$SKA (C.G.C)
=> SH=SK
=> $\frac{SH}{SB}=\frac{SK}{SD}$
=> HK//BD 
Theo phần b: BD vuông góc với (SAC)
=> HK vuông góc với (SAC)
+ BD vuông góc với (SAC)=> BD vuông góc với AI, mà BD// HK
=> HK vuông góc với AI ( ĐPCM) 

c/ Theo cm ở câu a: BC vuông góc với (SAB) => BC vuông góc với AH, mà AH lại vuông góc với SB => AH vuông góc với (SBC) => AH vuông góc với SC (1)
Theo cm ở câu a: DC vuông góc với (SAD) => DC vuông góc với AK, mà AK lại vuông góc với SD => AK vuông góc với (SDC) => AK vuông góc với SC  (2)
Mặt khác theo giả thiết AI vuông góc với SC (3)
(1)(2)(3) => SC vuông góc với 3 đường thẳng AH, AI, AK => AH, AI, AK đồng phẳng (đpcm)

b/ BD vuông góc với AC (2 đường chéo của hình vuông)
BD vuông góc với SA (SA vuông góc với đáy)
=> BD vuông góc với mp(SAC) 

a/ 
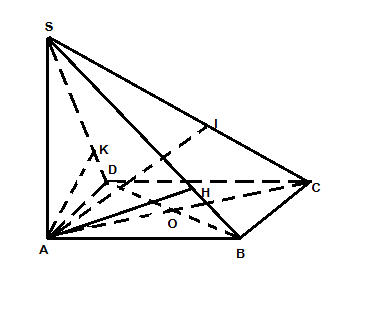
SA vuông góc với đáy => SA vuông góc với AB, AD => SAB, SAD là những tam giác vuông
SA cũng vuông góc với BC mà BC vuông góc với AB  => BC vuông góc với (SAB) => BC vuông góc với SB => SBC là tam giác vuông
SA cũng vuông góc với DC  mà DC vuông góc với AD  => DC vuông góc với (SAD) => DC vuông góc với SD => SDC là tam giác vuông (ĐPCM)