|
|
giải đáp
|
giai giup minh pai nay nha.thanks!
|
|
|
|
b/ Gắn hình vẽ vào trong hệ truch tọa độ sao cho A' trùng với gốc tọa độ A'B' trùng Ox, A'D' trùng Oy, A'A trùng Oz
Khi đó tọa đọ các điểm là: A'(0,0,0), D'(0,a,0), B'(a,0,0), M(a,3a/4,a), D(0,a,a)
Ta có: vector pháp tuyến của mp(DCC'D') là $\overrightarrow{A'D'}$(0,a,0)= (0,1,0)
vector pháp tuyến của mp(DMB') là tích có hướng của hai vector$\overrightarrow{DM}$ và vector $\overrightarrow{MB}$ là (-1,-4,3)
Khi đó, gọi X là góc giữa 2 mp(DMB') và mp(DCC'D')
cosX= $\frac{\left| {0.(-1)+1.(-4)+0.3} \right|}{\sqrt{(0^{2}+1^{2}+0^{2}).((-1)^{2}+(-4)^{2}+3^{2})}}$ = $\frac{4}{\sqrt{26}}$
Từ đó suy ra được góc X.
|
|
|
|
giải đáp
|
giai giup minh pai nay nha.thanks!
|
|
|
|
a/ Gọi H là trọng tâm của ADD'A', G là trọng tâm của ABB'A'
=> HG= $\frac{a}{\sqrt{2}}$
=> B'D'=2HG= a$\sqrt{2}$
=> cạnh hình lập phương bằng a
=> $V_{hình lập phương}$ = $a^{3}$
|
|
|
|
giải đáp
|
đố nhé
|
|
|
|
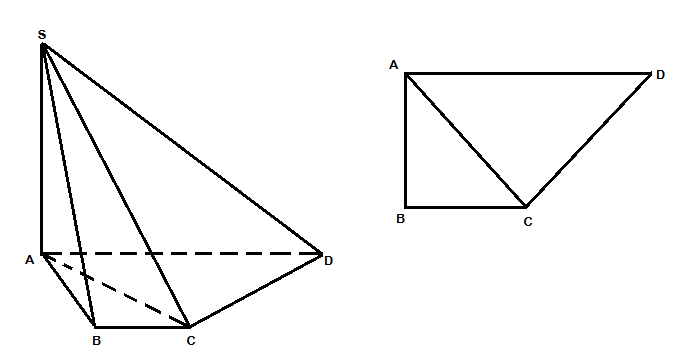 Dễ dàng chứng minh được DC vuông góc với ACmà DC vuông gocw vsới SA=> DC vuông góc với (SAC) => DC vuông góc với SC=> Góc tạo bởi mp (SDC) với mp(ABCD) là góc $\widehat{SCA}=60^{0}$Trong $\Delta$SAC vuông tại A, cạnh AC= a$\sqrt{2}$, $\widehat{SCA}=60^{0}$ => SA= AC. tan 60= a$\sqrt{6}$Lại có: $S_{ABCD}$= 1/2. (BC+AD).AB= $\frac{3a^{2}}{2}$=> $V_{SABCD}$= 1/3. SA. $S_{ABCD}$= $\frac{a^{3}.\sqrt{6}}{2}$ Dễ dàng chứng minh được DC vuông góc với ACmà DC vuông gocw vsới SA=> DC vuông góc với (SAC) => DC vuông góc với SC=> Góc tạo bởi mp (SDC) với mp(ABCD) là góc $\widehat{SCA}=60^{0}$Trong $\Delta$SAC vuông tại A, cạnh AC= a$\sqrt{2}$, $\widehat{SCA}=60^{0}$ => SA= AC. tan 60= a$\sqrt{6}$Lại có: $S_{ABCD}$= 1/2. (BC+AD).AB= $\frac{3a^{2}}{2}$=> $V_{SABCD}$= 1/3. SA. $S_{ABCD}$= $\frac{a^{3}.\sqrt{6}}{2}$ |
|
|
|
giải đáp
|
toán hình lớp 11
|
|
|
|
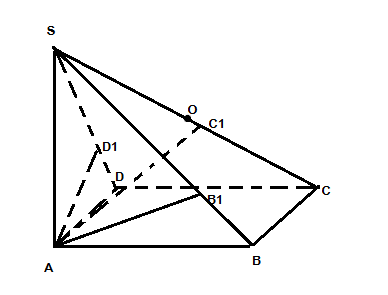
a/ Gọi O là trung điểm của SC
SA vuông góc với AC => $\Delta$SAC là tam
giác vuông tại A => OS= OC= OA= 1/2SC (1)
BC vuông góc với AB, BC vuông góc với
SA=> BC vuông góc với (SAB)=> BC vuông góc với SB =>
$\Delta$SBC vuông tại B => OS= OC= OB= 1/2 SC (2)
DC vuông góc với AD, DC vuông góc với
SA=> DC vuông góc với (SAD)=>DC vuông góc với SD =>
$\Delta$SDC vuông tại D => OS= OC= OD= 1/2 SC (3)
(1)(2)(3)=> O cách đều S, A,B,C,D một
khoảng bằng 1/2SC
Có: $SA^{2}+AC^{2}=SC^{2}$ => SC=
$a\sqrt{5}$ |
|
|
|
giải đáp
|
toán hình lớp 11
|
|
|
|
b/ BC vuông góc với (SAB)=>
BC vuông góc với AB1. Mà AB1 lại vuông góc với SB=> AB1 vuông
góc với mp(SBC)=> AB1 vuông góc với SC
Tương tự ta có AD1 vuông góc với SC
Theo giả thiết AC1 vuông góc với SC
=> A, B1,C1,D1 cùng thuộc một mặt phẳng
vuông góc với SC
|
|
|
|
giải đáp
|
toán hình lớp 11
|
|
|
|
c/ 2 mp(SDC) và mp(ABCD) có giao tuyến là
DC
Trong mp(ABCD) có AD vuông góc với DC
Theo chứng minh trên, trong mp(SDC) có SD
vuông góc với DC
=> Góc giữa mp(SDC) và mp(ABCD) là
$\widehat{SDA}$
Có: tanSDA= $\frac{SA}{AD}$=
$\frac{1}{\sqrt{3}}$ => SDA= 30
|
|
|
|
giải đáp
|
TOÁN HÌNH LỚP 11
|
|
|
|
BÀI 2: 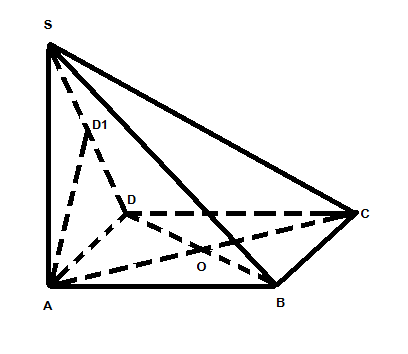 a/ SA vuông góc với AB => $\Delta$SAB là tam giác vuông SA vuông góc với AD => $\Delta$SAD là tam giác vuông SA vuông góc với BC mà BC vuông góc với AB => CB vuông góc vứoi (SAB)=> CB vuông góc vứoi SB => $\Delta$ SBC là tam giác vuông SA vuông góc với DC mà DC vuông góc với AD => CD vuông góc vứoi (SAD)=> CD vuông góc vứoi SD => $\Delta$ SDC là tam giác vuông b/ CD vuông góc với mp(SAD) => CD vuông góc vứoi AD1 Mà AD1 là đường cao trong tam giác SAD cân tại A (AS=AD=a) => AD1 vuông góc với SD => AD1 vuông góc với (SDC) |
|
|
|
giải đáp
|
TOÁN HÌNH LỚP 11
|
|
|
|
BÀI 1: 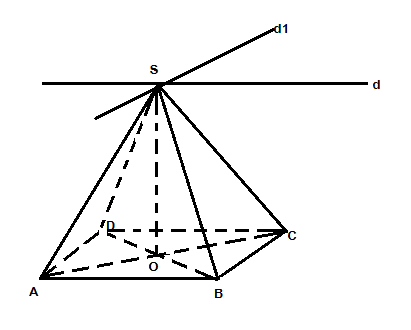 a/ SA= SC => $\Delta$SAC cân tại S => trung tuyến SO vuông góc với AC Tương tự SO vuông góc với BD => SO vuông góc ới mp (ABCD) b/ (d)= (SAB)$\cap $(SCD), mà AB// CD => giao tuyến d // AB// CD (d1)= (SCB)$\cap $(SAD), mà AD// CB=> giao tuyến d1 // AD// CB => mp(d, d1)// mp(ABCD) Mà SO vuông góc với (ABCD) => SO vuông góc với mp(d, d1) |
|
|
|
|
|
giải đáp
|
toán hình lớp 11
|
|
|
|
Bài này không làm được bạn nhé. Đề bài nếu có sửa lại như trên thì vẫn có sai sót
Vì AD= a do đáy là hình vuông cạnh a
SA=a do tam giác SAB là tam giác đều cạnh AB= a
Mà theo giả thiết, tam giác SAD là tam giác cân tại S => SD= SA=a
=> SA= SD= AD =a => SAD là tam giác đều, trái với giả thiết SAD là tam giác vuông cân tại S
|
|
|
|
giải đáp
|
các bác chỉ giùm e bài nè với
|
|
|
|
a/ Ta có: SB= a$\sqrt{10}$, SD= a$\sqrt{13}$
BC vuông gọc với AB, BC vuông gọc với SA => BC vuông gọc với (SAB)=> $\Delta$SBC là tam giác vuông tại B
Tương tự, tam giác SDC là tam giác vuông tại D
=> $S_{xq}$= $S_{SAB}$+ $S_{SBC}$+ $S_{SDC}$+$S_{SAD}$ = 1/2. (AS.AB+ BC. SB+DC. SD+AD.SA)= 1/2.(3a.a+2a.a$\sqrt{10}$+a. a$\sqrt{13}$+2a.3a)= 1/2.(11+$\sqrt{10}$+$\sqrt{13}$). $a^{2}$
|
|
|
|
giải đáp
|
hình học lớp 11
|
|
|
|
http://toan.hoctainha.vn/Hoi-Dap/Cau-Hoi/115687/toa-n-hi-nh-lo-p-11/15746#15746
Bạn tham khảo tại link này nhé, bài này giống với bài 3 mặc dù đề bài có hơi khác một chút, một bài đáy ABCD là hình chữ nhật, một bài đáy ABCD là hình vuông nhưng giả thiết đó không ảnh hưởng đến lời giải nhé!
|
|
|
|
giải đáp
|
Vecto trong không gian.
|
|
|
|
Bài này sẽ không có lời giải đâu nhé, mình vẽ hình đây. Bạn xem đi, không thể thẳng hàng được đúng không. Thứ nhất thừa giả thiết cho điểm F Thứ hai, mình nghĩ có thể bạn sai 1 dấu nào đó trong các đẳng thức vector trên 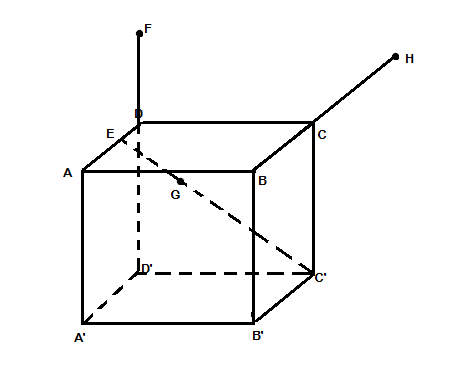 |
|
|
|
giải đáp
|
Hình học phẳng.
|
|
|
|
1/ Gọi (d1): x+y-2=0
(d2): 9x-3y-4=0
Ta có: AB qua A(2,2) và vuông góc với (d2) => VTPT của AB là (3,9)=3.(1,3)
=> Phương trình đường AB là: x+3y-8=0
Có B là giao của AB và (d1)
Từ đó, tọa độ của B là nghiệm của hệ phương trình:
$\begin{cases}x+3y-8=0 \\ x+y-2=0 \end{cases}$
=> $\begin{cases}x=7/2 \\ y= 3/2\end{cases}$
Vậy tọa độ của B là (7/2, 3/2)
|
|
|
|
giải đáp
|
Hình học phẳng.
|
|
|
|
2/ Gọi I (x,y) là tâm đường tròn đi qua 3 điểm A, B,C
Có: $\overrightarrow{IA}$ (1-x,2-y) => $IA^{2}$= $(1-x)^{2}+(2-y)^{2}$
$\overrightarrow{IB}$ (5-x,2-y) => $IB^{2}$= $(5-x)^{2}+(2-y)^{2}$
$\overrightarrow{IC}$ (1-x,3-y) => $IC^{2}$= $(1-x)^{2}+(3-y)^{2}$
Xét hệ:
$\begin{cases}(1-x)^{2}+(2-y)^{2}= (5-x)^{2}+(2-y)^{2}\\ (5-x)^{2}+(2-y)^{2}=(1-x)^{2}+(3-y)^{2} \end{cases}$
=> $\begin{cases}x=3 \\ y=5/2 \end{cases}$
Vậy I(3, 5/2)
|
|