|
|
giải đáp
|
toán hình lớp 11
|
|
|
|
BÀI 1:  a/ BC vuông góc với AB, BC vuông góc với SA => BC vuông góc với (SAB) b/ Do BC vuông góc với (SAB)=> BC vuông góc với AB' Mà AB' vuông góc với SB => AB' vuông góc với (SBC) c/ Do BC vuông góc với (SAB)=> BC vuông góc với SB => $\Delta$B'BC là tam giác vuông tịa B => B', B, C nằm trên đường tròn tâm G là trung điểm của B'C bán kính bằng 1/2B'C (1) Do AB' vuông góc với (SBC)=> AB' vuông góc với SC Mà SC lại vuông góc với AC' => SC vuông góc với (AB'C')=> SC vuông góc với B'C' => $\Delta$CC'B' là tam giác vuông tại C' => C, C', B' nằm trên đường tròn (G, 1/2B'C) (2) (1)(2)=> C,B, B', C' nằm trên cùng một đường tròn Vậy CBB'C' là tứ giác nội tiếp |
|
|
|
giải đáp
|
toán hình lớp 11
|
|
|
|
BÀI 2:  ABC. A'B'C' là lăng trụ đều có tất cả các cạnh bằng a => lăng trụ ABC. A'B'C' cũng là lăng trụ đứng Gọi I là trung điểm của B'C' Dễ dàng chứng minh được B'M vuông góc với BI (1) Lại có: A'I vuông góc với B'C', A'I vuông góc với BB' => A'I vuông góc với (BCC'B') => A'I vuông góc với B'M (2) (1)(2)=> B'M vuông góc với (BIA')=> B'M vuông góc với BA' |
|
|
|
giải đáp
|
toán hình lớp 11
|
|
|
|
BÀI 3:  a/ BD vuông góc với AC (2 đường chéo trong hình vuông vuông góc với nhau) BD vuông góc với SA do SA vuông góc vứoi đáy => BD vuông góc với (SAC) (1) Dễ dàng chứng minh được SB'= SD' => $\frac{SB'}{SB}=\frac{SD'}{SD}$=> B'D'// BD (2) (1)(2)=> B'D' vuông góc với (SAC) b/ BC vuông góc với AB, BC vuông góc với SA=> BC vuông góc với (SAB)=> BC vuông góc với AB', mà AB' vuông góc với SB=> AB' vuông góc với SC (3) DC vuông góc với AD, DC vuông góc với SA=> DC vuông góc với (SAD)=> DC vuông góc với AD', mà AD' vuông góc với SD=> AD' vuông góc với SC (4) Theo giả thiết: AC' vuông góc với SC (5) (3)(4)(5)=> AB', AC', AD' đồng phẳng hay A, B', C', D' đồng phẳng c/ AB' vuông góc với (SBC)=> AB' vuông góc với B'C' => $\Delta$AB'C' vuông tại B' => A, B', C' nằm trên đường tròn tâm I là trung điểm của AC' bán kính bằng 1/2AC' Tương tự: A, D'C' nằm trên đường tròn (I, 1/2AC') Vậy AB'C'D' nội tiếp |
|
|
|
giải đáp
|
toán hình lớp 11
|
|
|
|
BÀI 4: 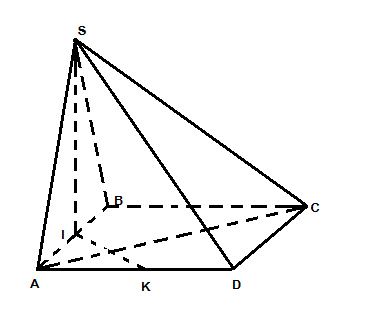 a/ Gọi I là trung điểm của BA Ta có $\Delta$BIC vuông tại B => $CI^{2}= BI^{2}+BC^{2}$ =$\frac{5a^{2}}{4}$ SI là trung tuyến trong tam giác SAB đều cạnh a=> SI= $\frac{a\sqrt{3}}{2}$ => $SI^{2}$= $\frac{3a^{2}}{4}$ Mặt khác: SC= a$\sqrt{2}$=> $SC^{2}= 2a$ Ta thấy: $CI^{2}$+ $SI^{2}$= $SC^{2}$ => $\Delta$SIC vuông tại C => SI vuông góc với IC, mà SI vuông góc với BA => SI vuông góc với (ABCD) Hai mp (SBA) và mp (ABCD) có chung tuyến là AB mà có SI vuông góc với (ABCD) theo chung tuyến AB => (SBA) vuông góc với (ABCD) b/ Có AC vuông góc với BD=> AC vuông góc với IK Mà AC vuông góc với SI do SI vuông góc với (ABCD) => AC vuông góc với (SIK)=> AC vuông góc với SK CM tương tự với ý còn lại |
|
|
|
giải đáp
|
Hình 12 - Bài 1
|
|
|
|
Lời giải này có yêu cầu trả vỏ sò để xem. Bạn hãy link trên để vào xem chi tiết
|
|
|
|
giải đáp
|
Hình 12 - Bài 2
|
|
|
|
Lời giải này có yêu cầu trả vỏ sò để xem. Bạn hãy link trên để vào xem chi tiết
|
|
|
|
giải đáp
|
hình 11
|
|
|
|
3/ Gọi I là trung điểm của SC. Ta sẽd chứng minh I cách đều 5 điểm S, A,B, C, D
$\Delta$ SBC, $\Delta$ SAC, $\Delta$ SDC là các tam giác vuông => IS= IC=IB=IA=ID= 1/2 SC
Như vậy, I cách đều 5 điểm S, A,B, C,D.
|
|
|
|
giải đáp
|
hình 11
|
|
|
|
2/ BC vuông góc với mp(SAB) => BC vuông góc với AH, MÀ AH vuông góc với SB => AH vuông góc với mp(SBC)=> AH vuông góc với SC(1)
DC vuông góc với mp(SAD) => DC vuông góc với AE, MÀ AE vuông góc với SD => AE vuông góc với mp(SDC)=> AE vuông góc với SC (2)
Theo giả thiết AK vuông góc với SC (3)
(1)(2)(3)=> AE, AK, AH cùng nằm trên mp vuông góc với SC
=> A, E, K, H đồng phẳng (đpcm)
|
|
|
|
giải đáp
|
hình 11
|
|
|
|
1/ SA vuông góc với đáy
=> SA vuông góc với AB => $\Delta$SAB là tam giác vuông
SA vuông góc với AD => $\Delta$SAD là tam giác vuông
SA vuông góc với BC mà BC vuông góc với AB => BC vuông góc với mp(SAB) => BC vuông góc với SB => $\Delta$ SBC là tam giác vuông
SA vuông góc với DC mà DC vuông góc với AD => DC vuông góc với mp(SAD) => DC vuông góc với SD => $\Delta$ SDC là tam giác vuông
|
|
|
|
giải đáp
|
câu hỏi toán học
|
|
|
|
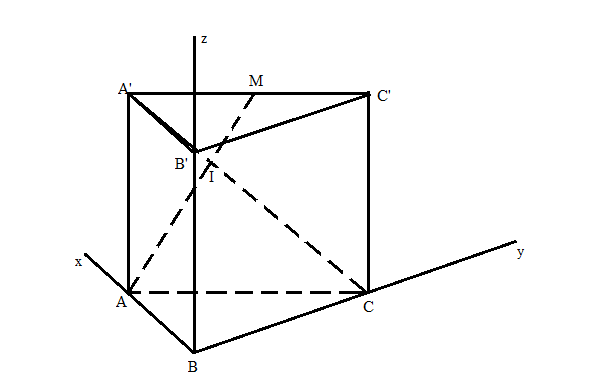 Xét $\Delta$A'AC vuông tại A => $AC^{2}= (3a)^{2}- (2a)^{2}= 5a^{2}$ Xét $\Delta$ABC vuông tại B => $BC^{2}= 5a^{2}- a^{2}= 4a^{2}$ => BC= 2a Gắn hệ trục tọa độ vào hình vẽ sao cho B trùng gốc tọa độ, BA trùng Ox, BC trùng Oy, BB' trùng Oz Khi đó tọa độ các điểm là: B(0,0,0), A'(a, 0, 2a), C(0, 2a, 0), A(a, 0,0), M(a/2, a, 2a) => $\overrightarrow{AM}$ (-a/2, a, 2a)= (-1,2,4) => Phương trình AM $\begin{cases}x= a-t_{1} \\ y=2t_{1}\\z=4t_{1} \end{cases}$ $\overrightarrow{A'C}$ (-a, 2a, -2a)= (1,-2,2) => Phương trình A'C $\begin{cases}x= t_{2} \\ y= 2a-2t_{2}\\z=2t_{2} \end{cases}$ Có: I= AM$\cap $A'C => Tọa độ I thỏa mãn : $\begin{cases}a-t_{1}= t_{2} \\ 2t_{1}=2a-2t_{2}\\4t_{1}=2t_{2} \end{cases}$ => $\begin{cases} t_{1}= a/3\\ t_{2}= 2a/3 \end{cases}$ => I(2a/3, 2a/3, 4a/3) Lại có phương trình mp(A'AB) là: y=0 => d(I, (A'AB)) = $\frac{\left| {2a/3} \right|}{\sqrt{1}}$= 2a/3 Mà: $S_{A'AB}$ = 1/2. AA'. AB= $a^{2}$ => $V_{IAA'B}$= 1/3. d(I, (A'AB)) . $S_{A'AB}$ = $\frac{2a^{2}}{9}$ |
|
|
|
giải đáp
|
cấp số cộng
|
|
|
|
Trong cấp số cộng thì 1 số bằng trung bình cộng 2 số liền kề
=> a= $\frac{-1+3}{2}$= 1
Khi đó: 3= $\frac{1+b}{2}$ => b=5
|
|
|
|
|
|
giải đáp
|
hơi khó các anh ạ
|
|
|
|
b/ Ý tưởng chứng minh: Để chứng minh 2 mp vuông góc với nhau ta chứng minh trong 2 mp đó chứa 2 cặp cạnh vuông góc với nhau. +) Chứng minh: (SAB) vuông góc với (SAD) AB vuông góc với AD, AB vuông góc với SA => AB vuông góc với (SAD)=> AB vuông góc với SD (1) AD vuông góc với AB, AD vuông góc với SA => AD vuông góc với (SAB)=> AD vuông góc với SB (2) (1)(2) => (SAB) vuông góc với (SAD) +) Chứng minh: (SAC) vuông góc với (SCD) tương tự như trên gợi ý : 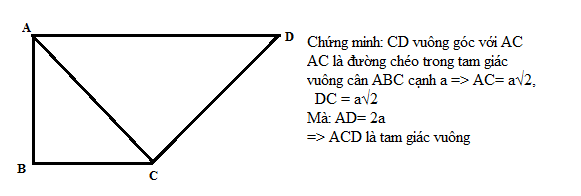 |
|
|
|
giải đáp
|
hơi khó các anh ạ
|
|
|
|
a/ (SAB) vuông góc với mp (ABCD)
(SAD) vuông góc với mp(ABCD)
=> đường vuông góc chung của 2 mp(SAB) và mp(SAD) là SA vuông góc với (ABCD) (đpcm)
|
|
|
|
giải đáp
|
Bài toán mặt phẳng song song với mặt phẳng(2).
|
|
|
|
c/ Trong mp(ABB'A'), kẻ MG//PN (G$\in $BB')
Khi đó: MPNG chính là thiết diện của (MNP) với hình hộp
Ta có: MPNG là hình bình hành (vì dễ dàng chứng minh được MG=PN)
P/S: lời giải này được áp dụng cho chương trình lớp 12!
|
|