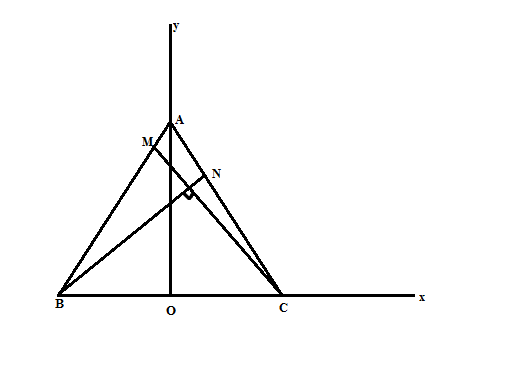
Gắn hệ trục tọa độ vào hình vẽ sao cho gốc O trùng với trung điểm của BC, OC trùng với Ox, OA trùng với Oy. Khi đó, tọa độ các điểm sẽ là: C(a/2, 0), B(-a/2,0), A(0, $\frac{a\sqrt{3}}{2}$)
Do, AN= 1/3AC => Tọa độ của N là: N(a/6,$\frac{a\sqrt{3}}{3}$ )
Từ đó, phương trình AB: $\sqrt{3}$x-y+ $\frac{a\sqrt{3}}{2}$=0
M$\in $AB=> M(x, $\sqrt{3}$x+$\frac{a\sqrt{3}}{2}$)
=> $\overrightarrow{CM}$ (x- a/2, $\sqrt{3}$x+$\frac{a\sqrt{3}}{2}$)
Mà $\overrightarrow{BN}$(2a/3, $\frac{a\sqrt{3}}{3}$ )
Vì BN vuông góc với CM => $\overrightarrow{BN}$. $\overrightarrow{CM}$=0 => x= -a/10
=> M(-a/10, $\frac{2a\sqrt{3}}{5}$ )
=> $\overrightarrow{AM}$ (-a/10, $\frac{-a\sqrt{3}}{10}$)
=> AM= a/5