|
|
giải đáp
|
Giúp mình bài hình này với :((
|
|
|
|
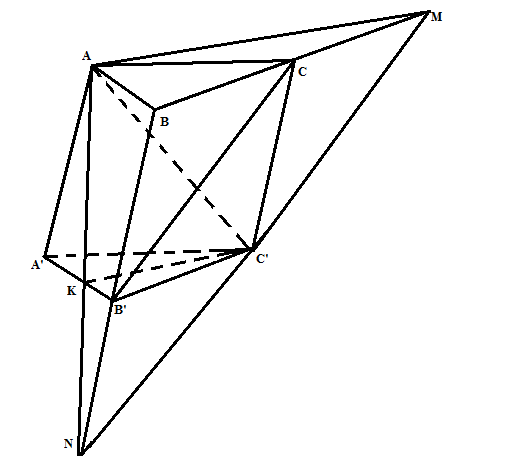 a/ Trong mp (BCC'B') qua C' kẻ đường thẳng song song với B'C cắt BC tại M, cắt BB' tại N Ta được mp(P) chính là mp(AMN) qua AC' và song song với CB' Trong mp(ABB'A') gọi K= AN$\cap $A'B' Khi đó thiết diện của hình lặng trụ với mp(P) là mp(AKC') |
|
|
|
|
|
bình luận
|
Bài toán khó về thiết diện hình chóp. (*)
:) Em nghĩ là nên làm tường minh 1 chút thôi. " Đối xứng lệch"- cụm từ đúng là em chưa nghe bao giờ luôn, hình như là không phổ biến, chỉ áp dụng cho HSG thôi thì phải!
|
|
|
|
|
|
|
|
|
|
sửa đổi
|
Tứ diện $ABCD$.
|
|
|
|
Gọi G, H là trung điểm của DC, DBM, N là trong tâm $\Delta$ABD, $\Delta$ADC=>AN/ AG= AM/AH= 2/3=> MN// GH=> MN//(BCD)
Gọi G, H là trung điểm của DC, DBM, N là trong tâm $\Delta$ABD, $\Delta$ADC=>AN/ AG= AM/AH= 2/3=> MN// GH=> MN//(BCD)
|
|
|
|
|
|
giải đáp
|
Bài toán khó về thiết diện hình chóp. (*)
|
|
|
|
a/PQ là giao tuyến của (SBC) và (α)⇒PQ∥BC
NM là giao tuyến của (ABCD) và (α)⇒NM∥BC
Suy ra PQ∥NM nên MNPQ là hình thang. (1)
Mặt khác, CN/ CD= NP/ SD= BM/BA= MQ/SA
Mà SA=SD dó $\Delta$SAD đều
=> MQ=NP(2)
(1)(2)=> MNPQ là hình thang cân
|
|
|
|
|
|
sửa đổi
|
Bài toán khó về thiết diện hình chóp. (*)
|
|
|
|
a) $PQ$ là giao tuyến của $(SBC) $ và $(\alpha) \Rightarrow PQ \parallel BC$$NM$ là giao tuyến của $(ABCD) $ và $(\alpha) \Rightarrow NM \parallel BC$Suy ra $PQ \parallel NM$ nên $MNPQ$ là hình thang.Mặt khác tương tự như trên ta cũng chứng minh được $MQ \parallel SA, ND \parallel SD.$Trong $\triangle SAB$ có $MQ \parallel SA\Rightarrow MQ < SA =AD < MN$ nên $MNPQ$ không thể là hình bình hành.Mà theo tính chất đối xứng $MQ=NP$ suy ra $MNPQ$ là hình thang cân với đáy lớn $MN$.
a) $PQ$ là giao tuyến của $(SBC) $ và $(\alpha) \Rightarrow PQ \parallel BC$$NM$ là giao tuyến của $(ABCD) $ và $(\alpha) \Rightarrow NM \parallel BC$Suy ra $PQ \parallel NM$ nên $MNPQ$ là hình thang.Mặt khác tương tự như trên ta cũng chứng minh được $MQ \parallel SA, NP \parallel SD.$Trong $\triangle SAB$ có $MQ \parallel SA\Rightarrow MQ < SA =AD < MN$ nên $MNPQ$ không thể là hình bình hành.Mà theo tính chất đối xứng $MQ=NP$ suy ra $MNPQ$ là hình thang cân với đáy lớn $MN$.
|
|
|
|
sửa đổi
|
Hình chóp.
|
|
|
|
b/ MP là đường trung bình trong $\Delta$ SAB => MP// SB => SB// (MNP)MN// AD=> Giao tuyến của (MNP) qua P và // AD cắt SD tại Q => SQ/ SD= SP/SA= 1/2 => Q là trung điểm của SD=> QN là đường trung bình trong $\Delta$SDC => SC// QN => SC// (MNQP)(đpcm)
b/ MP là đường trung bình trong $\Delta$ SAB => MP// SB => SB// (MNP)MN// AD=> Giao tuyến của (MNP) qua P và // AD cắt SD tại Q => SQ/ SD= SP/SA= 1/2 => Q là trung điểm của SD=> QN là đường trung bình trong $\Delta$SDC => SC// QN => SC// (MNQP)(đpcm)
|
|
|
|
giải đáp
|
Hình chóp.
|
|
|
|
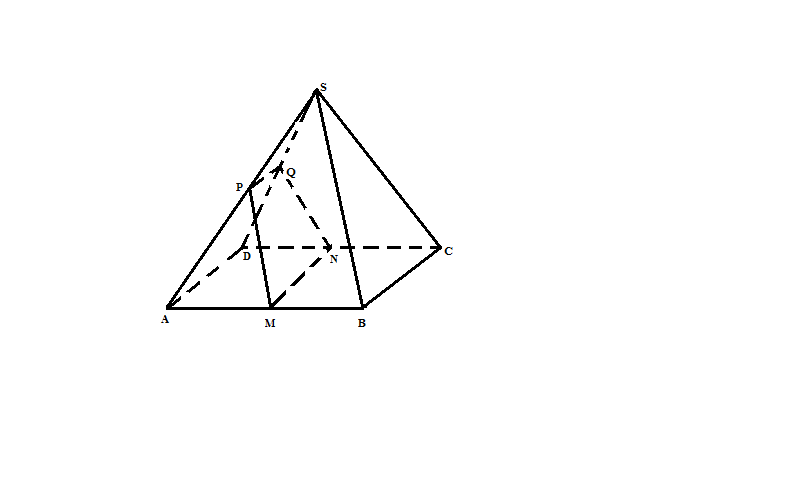 b/ MP là đường trung bình trong $\Delta$ SAB => MP// SB => SB// (MNP) MN// AD=> Giao tuyến của (MNP) qua P và // AD cắt SD tại Q => SQ/ SD= SP/SA= 1/2 => Q là trung điểm của SD => QN là đường trung bình trong $\Delta$SDC => SC// QN => SC// (MNQP) (đpcm) |
|
|
|
giải đáp
|
Hình chóp.
|
|
|
|
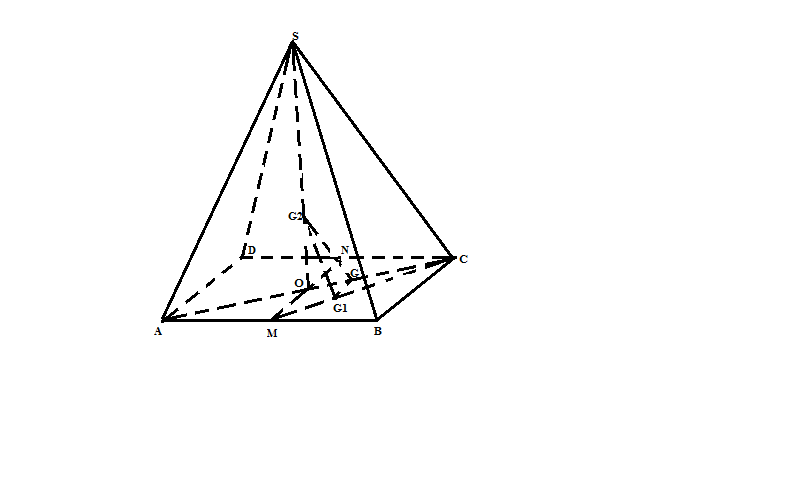 c/ Gọi O= MN$\cap $AC G1, G2 là trong tâm $\Delta$ABC và $\Delta$SAC => CG1/ CM= 2/3= SG2/SO (1) Trong mp(ABC) kẻ G1H// MO (3)=> CH/ CO= 2/3 (2) (1)(2)=> HG2// SC (4) (3), (4) => (G1HG2)// (SBC) => G1G2// (SBC) (đpcm) |
|
|
|
giải đáp
|
Hình chóp với thiết diện.
|
|
|
|
b/ MN// AD//BC=> DN/ DC= AM/AB (1)
KQ//AD => DQ/DS= AK/AS(2)
MK//SB => AH/AB = AK/AS (3)
(1)(2)(3)=> DN/DC= DQ/DS
=> QN// SC
=> SC// ($\alpha$)
|
|
|
|
giải đáp
|
Hình chóp với thiết diện.
|
|
|
|
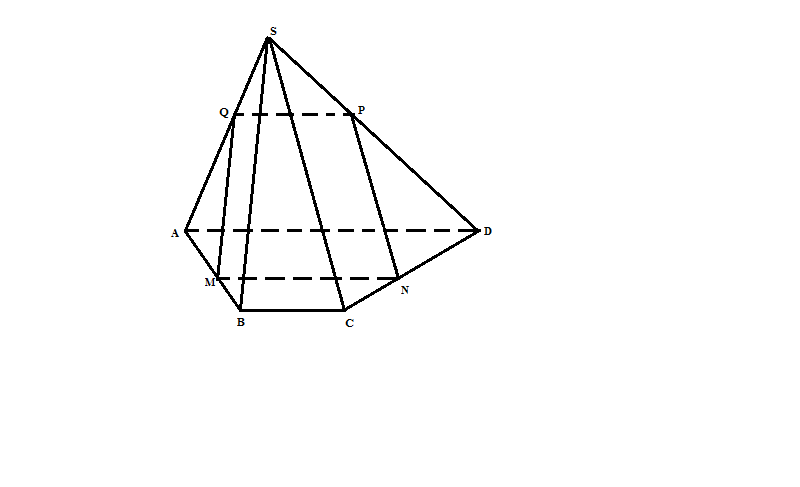 a/ Trong mp(ABCD) kẻ MN// AD (N$\in $DC) Trong mp(SAB) kẻ MK// SB (K$\in $SA) Khi đó($\alpha$) chính là (KMN) Vì MN// AD => Giao tuyến của (\alpha) với mp(SAD) qua K và song song với AD cắt SD tại Q Vậy thiết diện của $\alpha$ với hình chóp là (MNQK) |
|
|
|
giải đáp
|
Tứ diện.
|
|
|
|
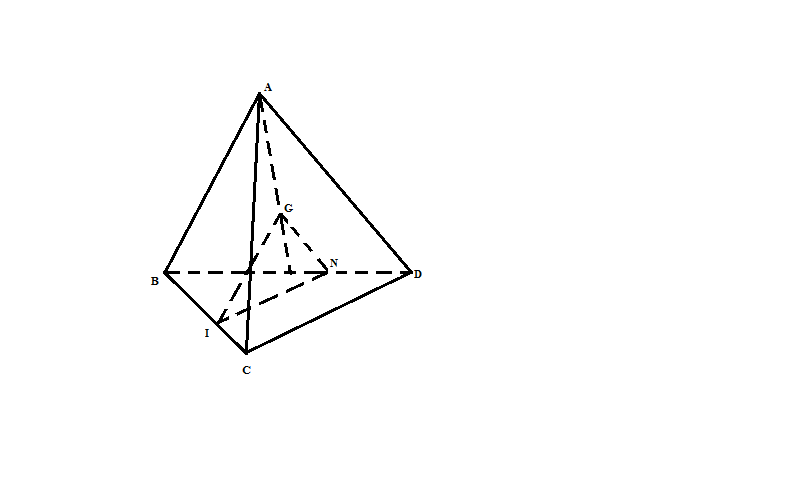 Có CI/ CB= 1/3 Trong mp(BCD) kẻ IN// CD (N$\in $BD) (1) => DI/ DB= 1/3 Gọi H là trung điểm của BD=> AG/ AH= 2/3 => Có: DN/ DH= 2/3 => GN// AD (2) (1)(2)=> (IGN)//(ACD) => GI// (ACD) |
|