|
|
|
|
giải đáp
|
hình không giian
|
|
|
|
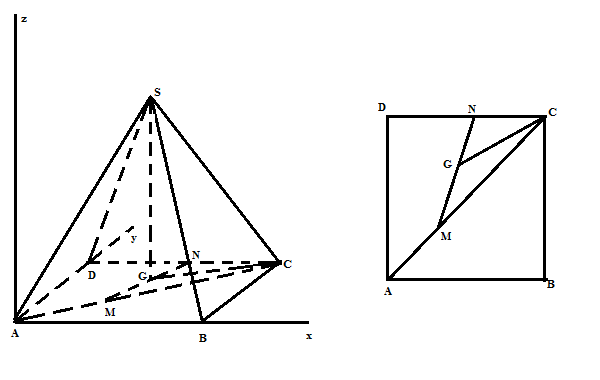 Gọi G là hình chiếu vuông góc của S xuống mp (ABCD) => SCGˆ= 600Gắn hình vẽ vào trong hệ trục tọa độ sao cho A trùng với gốc tọa độ, AB trùng với Ox, AD trùng với Oy, Oz là đường thẳng qua A và vuông góc với mp(ABCD)Khi đó tọa độ các điểm là: M(a/3, a/3, 0); C(a,a, 0); D(0,a,0); N(a/2,a,0)Có: G là trung điểm của MN => tọa độ G (5a/12, 2a/3, 0)=> GC−→− (7a/12, a/3, 0) => GC= 65√a12 Mà: ΔSGC vuông tại G => SG= GC. tan SCG= 195√a12 => Tọa độ S (5a12,2a3,195√a12) Từ đó, ta có khoảng cách h giữa DM và SN là: h= ∣∣[DM−→,SN−→].MN−→∣∣∣∣[DM−→,SN−→]∣∣ = 195√a543√ |
|
|
|
giải đáp
|
Đường thẳng song song mặt phẳng
|
|
|
|
Bài 2: 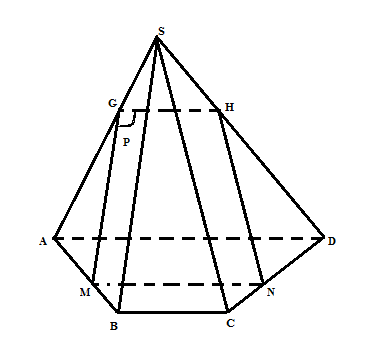 a/ Trong mp (ABCD) kẻ MN//AD (N$\in $CD) Trong mp(SAB) kẻ MH//SB (H$\in $SA) Khi đó: mp (P) chính là mp(HMN) Có: mp(P) //AD => giao tuyến của mp (P) với mp(SAD) cũng // với AD Trong mp(SAD), kẻ HG// AD (G$\in $SD) Vậy thiết diện của hình chóp với mp(P) chính là mp(HGNM) b/ Có: MN//AD//BC => $\frac{AM}{AB}=\frac{DN}{DC}$ (1) Có: HG// AD => $\frac{AH}{AS}= \frac{DG}{DS}$ (2) Có: MH// SB => $\frac{AM}{AB}=\frac{AH}{AS}$ (3) (1), (2), (3) => $\frac{DG}{DS}=\frac{DN}{DC}$ => SC// GN => SC// (P) (đpcm) |
|
|
|
giải đáp
|
Xác suất
|
|
|
|
b/ Các bộ phận B,C,D có diện tích bằng
nhau, A có diện tích gấp đôi B và máy bay bị trúng viên đạn
Xác suất để 1 viên đạn trúng vào một bộ
phận A,B,C,D lần lượt là: 0,4; 0,2; 0,2; 0,2
+) TH1: 2 viên đạn trúng vào cùng một bộ
phận
P(A)+p(B)+P(C)+P(D)= 2.P(A)+3.P(B)= 0,42 + 3. 0,22= 0,28
+) TH2: 2 viên đạn trúng vào 2 bộ phận liền
kề nhau
P(AB)+P(BA)+P(BC)+P(CB)+P(CD)+P(DC)
= 2. P(AB)+ 4. P(BC)
= 2.0,4.0,2+ 4.0,2.0,2= 0,32
Vậy xác suất để máy bay rơi là: 0,28+0,32=
0,6 |
|
|
|
giải đáp
|
Xác suất
|
|
|
|
a/ 4 bộ phận có diện tích bằng nhau và
máy bay bị trúng 2 viên đạn
Xác suất để 1 viên đạn trúng vào các bộ
phận A,B,C,D lần lượt là 0,25; 0,25; 0,25; 0,25.
+) TH1: 2 viên đạn trúng 2 bộ phận liền kề
P(AB)+P(BA)+P(BC)+P(CB)+P(CD)+P(DC) = 6. P(AB) =6.
O,25. 0,25= 0,375
+) TH2: 2 viên dạn cùng trúng vào một bộ
phận
P(A)+P(B)+P(C)+P(D)= 4. P(A)= 4. (0,25)2= 0,25
Vậy xác suất để máy bay rơi là: 0,375+0,25=
0,625 |
|
|
|
đặt câu hỏi
|
Tính tích phân!
|
|
|
|
Tính tích phân bằng cách tham số hóa đường cong (tính trực tiếp) hàm:
J= $\int\limits_{\gamma}^{}$ $\frac{e^{z}.dz}{z.(z-2i)}$, $\left\{ {\left| {z-3i} \right|=2} \right\}$
|
|
|
|
bình luận
|
hỏi chút
Lâu lắm rồi tớ ms lại thấy 1 bài hình hay như thế này :)
|
|
|
|
|
|
|
|
giải đáp
|
hỏi chút
|
|
|
|
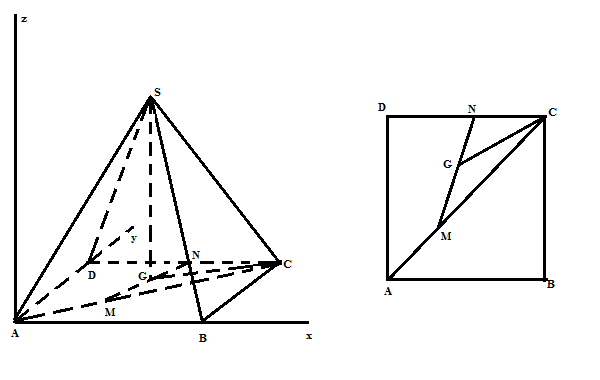 Gọi G là hình chiếu vuông góc của S xuống mp (ABCD) => $\widehat{SCG}$= $60^{0}$ Gắn hình vẽ vào trong hệ trục tọa độ sao cho A trùng với gốc tọa độ, AB trùng với Ox, AD trùng với Oy, Oz là đường thẳng qua A và vuông góc với mp(ABCD) Khi đó tọa độ các điểm là: M(a/3, a/3, 0); C(a,a, 0); D(0,a,0); N(a/2,a,0) Có: G là trung điểm của MN => tọa độ G (5a/12, 2a/3, 0) => $\overrightarrow{GC}$ (7a/12, a/3, 0) => GC= $\frac{\sqrt{65}a}{12}$ Mà: $\Delta$SGC vuông tại G => SG= GC. tan SCG= $\frac{\sqrt{195}a}{12}$ => Tọa độ S ($\frac{5a}{12}, \frac{2a}{3}, \frac{\sqrt{195}a}{12}$) Từ đó, ta có khoảng cách h giữa DM và SN là: h= $\frac{\left| {\left[ {\overrightarrow{DM},\overrightarrow{SN}} \right].\overrightarrow{MN}} \right|}{\left| {\left[ {\overrightarrow{DM},\overrightarrow{SN}} \right]} \right|}$ = $\frac{\sqrt{195}a}{5\sqrt{43}}$ |
|
|
|
bình luận
|
Giúp mình với!
Câu hỏi này cần xây dựng các miền đơn diệp bạn Khang ah, mở câu hỏi cho mình đi!
|
|
|
|
|
|
|
|
đặt câu hỏi
|
Giúp mình với!
|
|
|
|
Xét hàm số f(z)= $z^{\alpha}$, $\alpha\in $N ($\alpha$ tùy chọn) (N là tập số tự nhiên)
Xây dựng các miền $D_{1},D_{2},.....$ hữu hạn
sao cho f(z) đơn diệp trên từng miền và $\bigcup_{k\geqslant ...}^{}$ $\overline{D_{K}}$ = C (tập C- tập số phức)
Chú ý: trong dấu ba chấm trên là tùy ta xây dựng!
Thanksss so so much :)
|
|
|
|
giải đáp
|
jup mình nhé mọi người.thanks
|
|
|
|
AB, DC vuông góc với AD
=> Phương trình có dạng:
AB: $\sqrt{2}$.x-y+a=0
DC: $\sqrt{2}$.x-y+b=0
Tham số hóa các điểm: A($\sqrt{2}.y_{0}$, $y_{0}$) ; B($x_{0}$, $\sqrt{2}.x_{0}$+a); C($x_{1}$, $\sqrt{2}.x_{1}$+b)
Có M là trung điểm của BC => $\begin{cases}\frac{x_{0}+x_{1}}{2}=1 \\ \frac{\sqrt{2}.x_{0}+a+\sqrt{2}.x_{1}+b}{2}=0 \end{cases}$
=> b= -2.$\sqrt{2}$-a
=> Phương trình DC: $\sqrt{2}$.x-y-2.$\sqrt{2}$-a=0
=> d(M,DC)= $\frac{\left| {\sqrt{2}- 2.\sqrt{2}- a} \right|}{\sqrt{3}}$
d(B, DC)= $\frac{\left| {-2.\sqrt{2}-2a} \right|}{\sqrt{3}}$
Lại có: d(B,DC)= 2. d(M,DC)
=> $\left| {-2\sqrt{2}-2a} \right|$ = 2. $\left| {-\sqrt{2}-a} \right|$
=> a= -$\sqrt{2}$
=> Phương trình AB: $\sqrt{2}$.x-y- $\sqrt{2}$=0
=> Tọa độ A là nghiệm của hệ phương trình AB, AD: $\begin{cases}\sqrt{2}.x- y- \sqrt{2}=0 \\ x- \sqrt{2}.y= 0 \end{cases}$
=> A(2, $\sqrt{2}$)
|
|
|
|
giải đáp
|
HÌNH
|
|
|
|
Gợi ý cho câu D. Mình chưa nhìn ra câu d nhưng có 1 số gợi ý sau:
Gọi G= AK$\cap $ DO, M= CO$\cap $AK
Bạn hãy chứng minh: $\Delta$MGO đồng dạng với $\Delta$ MCK
Khi đó: $\widehat{MGO}$ = $\widehat{MCK}$ = $90^{0}$
=> đpcm
|
|
|
|
sửa đổi
|
Toán 9
|
|
|
|
Toán 9 1, Cho các số dương x,y,z thoả mãn \sqrt{x} + \sqrt{y} + \sqrt{z} = 0CMR \frac{1}{x+y-z} + \frac{1}{y+z-x} + \frac{1}{z+x-y} = 02, CMR Nếu \sqrt{x^{2}+\sqrt[3]{x^{4}.y^{2}} } + \sqrt{y^{2}+\sqrt[3]{y^{4}.x^{2}} } = a Thì \sqrt[3]{x^{2}} + \sqrt[3]{y^{2}} = \sqrt[3]{a^{2}}
Toán 9 1, Cho các số dương x,y,z thoả mãn $\sqrt{x} + \sqrt{y} + \sqrt{z} $ = 0CMR $\frac{1}{x+y-z} + \frac{1}{y+z-x} + \frac{1}{z+x-y} $ = 02, CMR Nếu $\sqrt{x^{2}+\sqrt[3]{x^{4}.y^{2}} } + \sqrt{y^{2}+\sqrt[3]{y^{4}.x^{2}} } $ = a Thì $\sqrt[3]{x^{2}} + \sqrt[3]{y^{2}} = \sqrt[3]{a^{2}} $
|
|
|
|
|
|
giải đáp
|
HÌNH
|
|
|
|
c/ $\Delta$IAO =$\Delta$ICO => $\widehat{IOA}$= $\widehat{IOC}$
$\Delta$OCK =$\Delta$OBK => $\widehat{COK}$= $\widehat{BOK}$
=> $\widehat{IOA}$+ $\widehat{BOK}$= 1/2.$180^{0}$= $90^{0}$
Mà $\widehat{IOA}$+ $\widehat{AIO}$= $90^{0}$
=> $\widehat{AIO}$= $\widehat{BOK}$
=> $\Delta$AIOđồng dạng với $\Delta$BOK (g-g)
=> $\frac{IA}{OB}$= $\frac{AO}{BK}$
=> IA. BK= AO.OB= $R^{2}$
|
|