|
|
giải đáp
|
giúp mình bài thể tích nhé
|
|
|
|
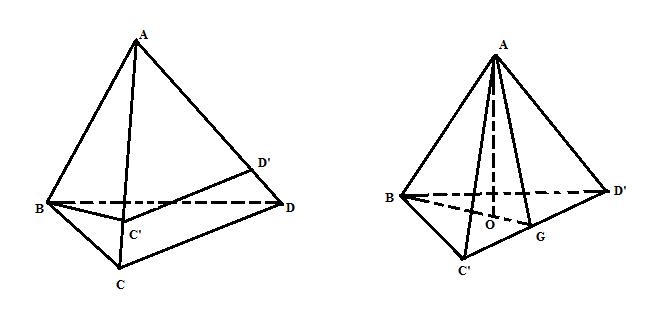 Trên AC lấy C' sao cho AC'= a, trên AD lấy D' sao cho AD'= a Khi đó ta đi tính thể tích tứ diện đều ABC'D' (do các mặt đều là tam giác đều) Gọi G là trung điểm C'D Gọi O là trọng tâm $\Delta$BC'D', ta có AO vuông góc với mp (BC'D') Xét $\Delta$AOG có $AO^{2}$= $AG^{2}$-$OG^{2}= $$(a\sqrt{3}/2)^{2}$ - $(\frac{a\sqrt{3}}{6})^{2}$= 4$a^{2}$/9 => AO=2a/3 Có $S_{BC'D'}$ =1/2. BG.C'D'= $\frac{a^{2}\sqrt{3}}{4}$ => $V_{A.BC'D'}$= $\frac{a^{3}\sqrt{3}}{18}$ Tỉ lệ thể tích giữa 2 khối chóp tam giác: $\frac{V_{ABC'D'}}{V_{ABCD}}$= $\frac{AB}{AB}$. $\frac{AC'}{AC}$. $\frac{AD'}{AD}$= a/b. a/c= $\frac{a^{2}}{bc}$ => $V_{ABCD}$= $\frac{abc\sqrt{3}}{18}$ |
|
|
|
sửa đổi
|
Các vấn đề liên quan đến bài toán tứ diện $ABCD$.
|
|
|
|
a/ Trong mp(BCD), gọi E= CD$\cap $JK. Khi đó, E =CD$\cap $(IJK)Có EJ qua K là trung tuyến trong $\Delta$BCE, mà BK= 2/3 BD=> K là trọng tâm $\Delta$BCE => BD là trung tuyến trong $\Delta$BCE=> DC = DEb/ Trong mp( ACE), gọi F= IE$\cap $ADTrong $\Delta$ACE có 2 trung tuyến EI và AD giao nhau tại F=> AF= 2FDc/ Có F là trọng tâm $\Delta$ACE => EF= 2/3. EICó K là trọng tâm $\Delta$BCE => EK= 2/3. EJ=> EF/EI = EK/EJ=> FK // IJ
a/ Trong mp(BCD), gọi E= CD$\cap $JK. Khi đó, E =CD$\cap $(IJK)Có EJ qua K là trung tuyến trong $\Delta$BCE, mà BK= 2/3 BD=> K là trọng tâm $\Delta$BCE => BD là trung tuyến trong $\Delta$BCE=> DC = DEb/ Trong mp( ACE), gọi F= IE$\cap $ADTrong $\Delta$ACE có 2 trung tuyến EI và AD giao nhau tại F=> AF= 2FDc/ Có F là trọng tâm $\Delta$ACE => EF= 2/3. EICó K là trọng tâm $\Delta$BCE => EK= 2/3. EJ=> EF/EI = EK/EJ=> FK // IJd/ Mp (IJK) được mở rộng thành mp (IJE)Có MN nằm trong mp (ABN)Trong mp(BCD), gọi O= BN$\cap $JKTrong mp(ACE), gọi G= AN$\cap $IE=> Giao tuyến giữ 2 mp(BCD) và mp(ACE) là OGTrong mp(ABN), gọi N =MN$\cap $OGKhi đó, N= MN$\cap $ mp(IJK)
|
|
|
|
bình luận
|
bài thể tích khối chóp :((
Có tỉ lệ thể tích giữa 2 khối chóp tam giác nhưng không có tỉ lệ giữa 2 khối chóp tứ giác!
|
|
|
|
|
|
|
|
sửa đổi
|
Các vấn đề liên quan đến bài toán tứ diện $ABCD$.
|
|
|
|
a/ Trong mp(BCD), gọi E= CD$\cap $JK. Khi đó, E =CD$\cap $(IJK)Có EJ qua K là trung tuyến trong $\Delta$BCE, mà BK= 2/3 BD=> K là trọng tâm $\Delta$BCE => BD là trung tuyến trong $\Delta$BCE=> DC = DEb/ Trong mp( ACE), gọi F= IE$\cap $ADTrong $\Delta$ACE có 2 trung tuyến EI và AD giao nhau tại F=> AF= 2FDc/ Có F là trọng tâm $\Delta$ACE => EF= 2/3. EICó K là trọng tâm $\Delta$BCE => EK= 2/3. EJ=> EF/EI = EK/EJ
a/ Trong mp(BCD), gọi E= CD$\cap $JK. Khi đó, E =CD$\cap $(IJK)Có EJ qua K là trung tuyến trong $\Delta$BCE, mà BK= 2/3 BD=> K là trọng tâm $\Delta$BCE => BD là trung tuyến trong $\Delta$BCE=> DC = DEb/ Trong mp( ACE), gọi F= IE$\cap $ADTrong $\Delta$ACE có 2 trung tuyến EI và AD giao nhau tại F=> AF= 2FDc/ Có F là trọng tâm $\Delta$ACE => EF= 2/3. EICó K là trọng tâm $\Delta$BCE => EK= 2/3. EJ=> EF/EI = EK/EJ=> FK // IJ
|
|
|
|
giải đáp
|
Các vấn đề liên quan đến bài toán tứ diện $ABCD$.
|
|
|
|
a/ Trong mp(BCD), gọi E= CD$\cap $JK. Khi đó, E =CD$\cap $(IJK)
Có EJ qua K là trung tuyến trong $\Delta$BCE, mà BK= 2/3 BD
=> K là trọng tâm $\Delta$BCE => BD là trung tuyến trong $\Delta$BCE=> DC = DE
b/ Trong mp( ACE), gọi F= IE$\cap $AD
Trong $\Delta$ACE có 2 trung tuyến EI và AD giao nhau tại F
=> AF= 2FD
c/ Có F là trọng tâm $\Delta$ACE => EF= 2/3. EI
Có K là trọng tâm $\Delta$BCE => EK= 2/3. EJ
=> EF/EI = EK/EJ
=> FK // IJ
d/ Mp (IJK) được mở rộng thành mp (IJE)
Có MN nằm trong mp (ABN)
Trong mp(BCD), gọi O= BN$\cap $JK
Trong mp(ACE), gọi G= AN$\cap $IE
=> Giao tuyến giữ 2 mp(BCD) và mp(ACE) là OG
Trong mp(ABN), gọi N =MN$\cap $OG
Khi đó, N= MN$\cap $ mp(IJK)
|
|
|
|
giải đáp
|
Bài toán về hình chóp $S.ABCD$.
|
|
|
|
a/ Trong mp (SCD), gọi K = SM $\cap $CD
Khi đó, mp( SBM) chính là mp (SBK)=> CD$\cap $ (SBM) = K
b/ Trong mp(ABCD) gọi O= AC$\cap $BD
Trong mp(SBK), họi G= SO$\cap $BM
Khi đó: G= BM$\cap $(SAC)
c/ Trong mp (SAC), gọi H= SO$\cap $AG
Khi đó, H= SC$\cap $ (ABM)
|
|
|
|
|
|
|
|
bình luận
|
bài thể tích khối chóp :((
Mình không nhớ công thức ấy tên là gì nhưng chắc chắn là không có tỉ lệ thể tích giữa 2 khối chóp tứ giác đâu. Đưa ra 1 lời giải sai sẽ ảnh hưởng đến cách suy nghĩ người đọc! Đây chỉ là ý kiến chủ quan của mình thôi.
|
|
|
|
|
|
|
|
sửa đổi
|
tính khoảng cách
|
|
|
|
AC= $\sqrt{AB^{2}+BC^{2}}$= 2$\sqrt{5}$aXét $\Delta$SAC vuông tại A, tan SAC= $\frac{SA}{AC}$= $\frac{\sqrt{3}}{3}$ => SA= $\frac{2\sqrt{15}a}{3}$Ghép hình với hệt rục tọa độ trong không gian, sao cho A trùng O, AB trùng Ox, AD trùng Oy, AS trùng OzKhi đó tọa độ các điểm là: A(0,0,0), B(2a,0,0), M(2a,2a,0), N(0,3a,0), S( 0,0, $\frac{2\sqrt{5}a}{3}$)Theo công thức tính khoảng cách 2 đường chéo nhau trong không gian thì: d( $\overrightarrow{SB}$, $\overrightarrow{MN}$)= $\frac{\left| {\left[ {\overrightarrow{SB},\overrightarrow{MN}} \right].\overrightarrow{MB}} \right|}{\left| {\left[ {\overrightarrow{SB},\overrightarrow{MN}} \right]} \right|}$= $\frac{4\sqrt{5}a}{\sqrt{34}}$
AC= $\sqrt{AB^{2}+BC^{2}}$= 2$\sqrt{5}$aXét $\Delta$SAC vuông tại A, tan SAC= $\frac{SA}{AC}$= $\frac{\sqrt{3}}{3}$ => SA= $\frac{2\sqrt{15}a}{3}$Ghép hình với hệt rục tọa độ trong không gian, sao cho A trùng O, AB trùng Ox, AD trùng Oy, AS trùng OzKhi đó tọa độ các điểm là: A(0,0,0), B(2a,0,0), M(2a,2a,0), N(0,3a,0), S( 0,0, $\frac{2\sqrt{5}a}{3}$)Theo công thức tính khoảng cách 2 đường chéo nhau trong không gian thì: d( $\overrightarrow{SB}$, $\overrightarrow{MN}$)= $\frac{\left| {\left[ {\overrightarrow{SB},\overrightarrow{MN}} \right].\overrightarrow{MB}} \right|}{\left| {\left[ {\overrightarrow{SB},\overrightarrow{MN}} \right]} \right|}$= $\frac{4\sqrt{5}a}{\sqrt{34}}$
|
|
|
|
giải đáp
|
tính khoảng cách
|
|
|
|
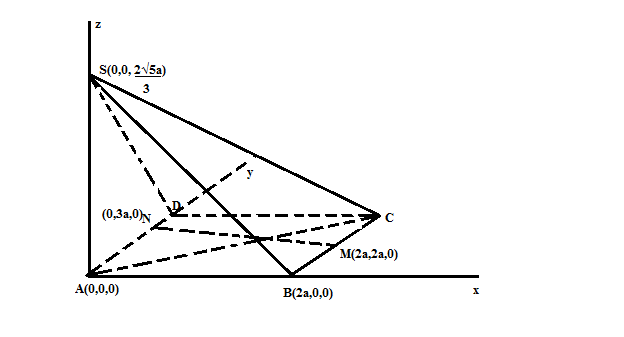 AC= $\sqrt{AB^{2}+BC^{2}}$= 2$\sqrt{5}$a Xét $\Delta$SAC vuông tại A, tan SAC= $\frac{SA}{AC}$= $\frac{\sqrt{3}}{3}$ => SA= $\frac{2\sqrt{15}a}{3}$ Ghép hình với hệt rục tọa độ trong không gian, sao cho A trùng O, AB trùng Ox, AD trùng Oy, AS trùng Oz Khi đó tọa độ các điểm là: A(0,0,0), B(2a,0,0), M(2a,2a,0), N(0,3a,0), S( 0,0, $\frac{2\sqrt{5}a}{3}$) Theo công thức tính khoảng cách 2 đường chéo nhau trong không gian thì: d( $\overrightarrow{SB}$, $\overrightarrow{MN}$)= $\frac{\left| {\left[ {\overrightarrow{SB},\overrightarrow{MN}} \right].\overrightarrow{MB}} \right|}{\left| {\left[ {\overrightarrow{SB},\overrightarrow{MN}} \right]} \right|}$= $\frac{4\sqrt{5}a}{\sqrt{34}}$ |
|
|
|
|
|
giải đáp
|
gai gjup mh voi
|
|
|
|
$\overrightarrow{OM}$= a. $\overrightarrow{OA}$+ (1-a). $\overrightarrow{OB}$ = a.( $\overrightarrow{OM}$+ $\overrightarrow{MA}$)+ (1-a). ($\overrightarrow{OM}$+$\overrightarrow{MB}$) => $\overrightarrow{0}$= a. $\overrightarrow{MA}$+ (1-a). $\overrightarrow{MB}$ => a. $\overrightarrow{MA}$= (a-1). $\overrightarrow{MB}$ => $\frac{\overrightarrow{MA}}{\overrightarrow{MB}}$= $\frac{a-1}{a}$<0 (Do khi M$\in $AB thì $\overrightarrow{MA}$ và $\overrightarrow{MB}$ trái chiều) => 0<a<1 |
|
|
|
|
|
bình luận
|
bài thể tích khối chóp :((
Chỉ có tỉ lệ thể tích giữa 2 hình chóp tam giác thôi chứ không có tỉ lệ thể tích giữa 2 hình chóp tứ giác đâu. Hơn nữa, giữa các tỉ lệ là phép nhân chứ không phải là phép cộng đâu.Nên lời giải này không hợp lý nhóe!
|
|
|
|
|
|