1)
$f(x)=\frac{1}{\sqrt[3]{(x+2)^2}+\sqrt[3]{x^2-4}+\sqrt[3]{(x-2)^2}    }=\frac{\sqrt[3]{x+2}-\sqrt[3]{x-2}}{(x+2)-(x-2)}=\frac{1}{4}\sqrt[3]{x+2}-\frac{1}{4}\sqrt[3]{x-2}$
Vậy $\int f(x)dx=\int \left (\frac{1}{4}\sqrt[3]{x+2}-\frac{1}{4}\sqrt[3]{x-2} \right )dx=\frac{3}{16}\sqrt[3]{(x+2)^4}-\frac{3}{16}\sqrt[3]{(x-2)^4}+C$

b) Ta có
$\begin{cases}0<x^2<1 \\ 0<e^{-x}<1 \end{cases}\Rightarrow 0<x^2e^{-x}<1$
Bạn tự chứng minh bài toán phụ sau coi như bài tập nhé.
Với $0<t<1$ thì $1-t<\frac{1}{1+t}<1-\frac{t}{2}$.
Áp dụng cho $t=x^2e^{-x}$ ta được
$\int\limits_{0}^{1} \left ( 1-x^2e^{-x} \right )dx \le \int\limits_{0}^{1} \frac{dx}{1+x^2e^{-x}}< \int\limits_{0}^{1} \left ( 1-\frac{1}{2}x^2e^{-x} \right )dx$
$\Leftrightarrow 1 - \int\limits_{0}^{1}x^2e^{-x}dx \leq  \int\limits_{0}^{1} \frac{dx}{1+x^2e^{-x}} < 1 -\frac{1}{2} \int\limits_{0}^{1}x^2e^{-x}dx.$

a) Áp dụng BĐT Bunhiacopski ta có
i) $\left (  \int\limits_{0}^{x}\sqrt{e^{2t} + e^{-t}}dt \right )^2=\left (  \int\limits_{0}^{x}e^{t/2}\sqrt{e^{t} + e^{-2t}}dt \right )^2\le \int\limits_{0}^{x}e^{t}dt. \int\limits_{0}^{x}\left (e^{t} + e^{-2t} \right )dt=(e^x-1)(e^x-\frac{1}{2})$
Vậy $\int\limits_{0}^{x}\sqrt{e^{2t} + e^{-t}}dt < \sqrt{(e^x-1)(e^x-\frac{1}{2})}$
ii) $\int\limits_{0}^{x}\sqrt{e^{2t} + e^{-t}}dt> \int\limits_{0}^{x}\sqrt{e^{2t}}dt=\int\limits_{0}^{x}e^{t}dt=e^x-1$
Vậy $\int\limits_{0}^{x}\sqrt{e^{2t} + e^{-t}}dt >e^x-1$

b) Dễ nhận thấy điểm $C$ có tọa độ $C(0;4)$
Ta có $S_{ABC}=1997\Leftrightarrow CO.AB=2.1997\Leftrightarrow 4.AB=2.1997\Leftrightarrow AB^2=\frac{1997^2}{4}$
$\Leftrightarrow (x_A-x_B)^2=\frac{1997^2}{4}\Leftrightarrow (x_A+x_B)^2-4x_Ax_B=\frac{1997^2}{4}$
Mặt khác thì $x_A, x_B$ là nghiệm của PT $x^2-2(m+1)x+4=0\Leftrightarrow \begin{cases}x_A+x_B=2(m+1) \\ x_Ax_B=4 \end{cases}$
Vậy ta có $4(m+1)^2-16=\frac{1997^2}{4}\Leftrightarrow m=-1 \pm\frac{\sqrt{3988073}}{4}$

a)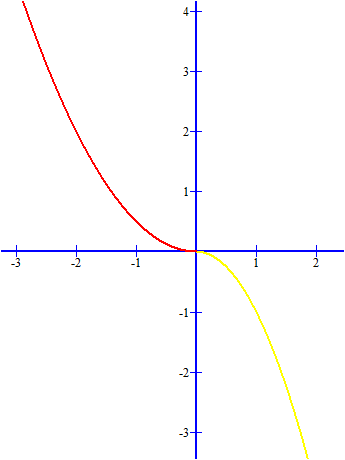

Đồ thị $y= \frac{1}{2}x^2$  khi $-3\leq x\leq 0$ có màu đỏ trên hình vẽ
Đồ thị $y= -x^2$  khi $0\leq x\leq 2$ có màu vàng trên hình vẽ

Đặt $a=\sqrt[3]{3(1+\sqrt[3]{2}+\sqrt[3]{4})},   b=\sqrt{\frac{1}{4}+\sqrt[3]{2}+\sqrt[3]{4}}$
Ta có điều sau :
$\sqrt[3]{3(1+\sqrt[3]{2}+\sqrt[3]{4})}-\sqrt{\frac{1}{4}+\sqrt[3]{2}+\sqrt[3]{4}}=\frac{1}{2}$
Bạn có thể tự chứng minh coi như bài tập nhé.
PT $\Leftrightarrow \sqrt[3]{3x^2-3x+3}-a=\sqrt{\frac{x^3}{3}-\frac{3}{4}}-b$
$\Leftrightarrow \frac{3(x+\sqrt[3]{2})(x-\sqrt[3]{2}-1)}{A^2+Aa+a^2}=\frac{(x-\sqrt[3]{2}-1)f(x)}{B+b}         (*)$
Trong đó $A=\sqrt[3]{3x^2-3x+3},       B=\sqrt{\frac{x^3}{3}-\frac{3}{4}}$
Kiểm tra rằng từ $(*)$ PT đã cho chỉ có nghiệm duy nhất $x=\sqrt[3]{2}+1$
Nếu bạn đang học phổ thông thì không nên lo lắng vì bài tập này do tính chất nghiệm không đơn giản. Còn nếu bạn đã làm quen với một số phần mềm để có thể kiểm tra được nghiệm của PT thì trên đây là câu trả lời có thể chấp nhận được.

từ HPT $\Rightarrow 11(x^{2}+3xy+y^{2})=12(x^{2}-3xy+3y^{2})\Leftrightarrow x^2-69xy+25y^2=0\Leftrightarrow x=\frac{1}{2}\left ( 69 \pm\sqrt{4661} \right )y$
Thay điều này vào PT thứ nhất ta được
$x=\pm\frac{5}{2}\sqrt{1-\sqrt{\frac{7}{11}}}$ và $y=\frac{2x}{ 69 \pm\sqrt{4661}}$

Lời giải này có yêu cầu trả vỏ sò để xem. Bạn hãy link trên để vào xem chi tiết