c/ c/ Gọi tọa độ C' là (x,y,z)
=> $\overrightarrow{AC'}$ =(x-1, y, z-1)
$\overrightarrow{CC'}$ =(x-1, y+1, z-1)
ABCC' là hình bình hành => AC'// BC, AB//CC'
 => $\begin{cases}\frac{x-1}{1}= \frac{y}{2}= \frac{z-1}{1} \\ \frac{x-1}{1}= \frac{y+1}{1}= \frac{z-1}{1} \end{cases}$
=> $\begin{cases}x=0 \\ y= -2\\ z= 0 \end{cases}$ 
Vậy tọa độ của C là: (0, -2, 0) 

b/ Xét tọa độ$\overrightarrow{AC}$, $\overrightarrow{AB}$ ta thấy: $\frac{0}{1}\neq \frac{-1}{1}\neq \frac{1}{1}$
=> A,B,C không thẳng hàng 

a/ $\overrightarrow{AB}$ (1,1,1)
$\overrightarrow{AC}$ (0,-1,1)
$\overrightarrow{BC}$ (-1,-2,-1)= (1,2,1)
$\overrightarrow{DC}$ (-3,-6,6)= (1,2,-2) 

Cách 2: Gắn hình vẽ vào tọa độ không gian (theo chương trình lớp 12)

Gọi N là trung điểm của CD
Vì (SAB) và (ABCD) nằm trong 2 mp vuông góc với nhau => trung tuyến SE trong tam giác đều SAB sẽ vuông góc với mp(ABCD)
Gắn hình vẽ vào tọa độ không gian sao cho E trùng với gốc tọa độ, EN trùng với Ox, EB trùng với Oy, ES trùng với Oz
Khoảng cách tù E đến mp(SCF) chính là d(E, (SCD))
Khi đó tọa độ các điểm là: E(0,0,0), S($0,0, \frac{a\sqrt{3}}{2}$) , C(a, a, 0), D(a/2, -a/2,0)
=> phương trình mp(SCD) => d(E, (SCD)) = $\frac{a\sqrt{3}}{\sqrt{7}}$a3√7√

Cách 1: Tính trực tiếp (theo chương trình lớp 11)

Vì (SAB) và (ABCD) nằm trong 2 mp vuông góc với nhau => trung tuyến SE trong tam giác đều SAB sẽ vuông góc với mp(ABCD)
Ta gọi G là trung điểm của CD, trong mp(SEG) kẻ EH vuông góc với SG ($H\in SG$)  (1)
Có: CD vuông góc với EG; CD vuông góc với SE => CD vuông góc với mp(SEG) => CD vuông góc vứoi EH (2)
(1)(2)=> EH vuông góc với (SCD) hay nói cách khác EH vuông góc với mp(SCF)
=> d(E, (SCF))= EH
Có: EH là đường cao trong $\Delta$SEG vuông tại E => $\frac{1}{EH^{2}}=\frac{1}{ES^{2}}+\frac{1}{EG^{2}}$ 
=>  $\frac{1}{EH^{2}}=\frac{1}{(\frac{a\sqrt{3}}{2})^{2}}+\frac{1}{a^{2}}$ 
=> EH= $\frac{a\sqrt{3}}{\sqrt{7}}$ 

K$\in$ (d) => K(x, 4-x)
=> d(K, $\Delta$) =$\frac{\left| {(1-m)^{2}.x+2m.(4-x)+m^{2}-4m-3} \right|}{\sqrt{(1-m^{2})^{2}+(2m)^{2}}}$ =1
=> $\frac{\left| {(1-4m+m^{2}).x+ m^{2}+4m-3} \right|}{m^{2}+1}$ =1
=> hoặc  ${(1-4m+m^{2}).x+ m^{2}+4m-3}$= $m^{2}+1$
hoặc ${(1-4m+m^{2}).x+ m^{2}+4m-3}$= $-m^{2}-1$ 
=> hoặc x= $\frac{4- 4m}{m^{2}-4m+1}$  hoặc  x= $\frac{-2m^{2}- 4m+2}{m^{2}-4m+1}$ 
Các điểm K cần t ìm là: K1($\frac{4- 4m}{m^{2}-4m+1}$ , $\frac{4m^{2}- 12m}{m^{2}-4m+1}$ ); K2($\frac{-2m^{2}- 4m+2}{m^{2}-4m+1}$ , $\frac{2m^{2}- 20m+6}{m^{2}-4m+1}$ )

1. ($x^{4}- x^{3}+ 6x^{2}- x- m$) = (x- 2). ($x^{3}+ x^{2}+ 8x+ 14$) + (28- m)
Để f(x) chia hết cho (x-2) thì (28- m)= 0
=> m=28 

Gọi số lớn là b, số bé là a
Theo giả thiết ta có: $\frac{a}{b}$= b-a= 0,75
=> a= 0,75b => b- 0,75b= 0,75 => 0,25b= 0,75 => b=3 => a= 2,25 

Lời giải này có yêu cầu trả vỏ sò để xem. Bạn hãy link trên để vào xem chi tiết

Trong mp(BCD) gọi G là giao điểm của CD và PK
Khi đó, G chính là giao điểm của CD và mp(MNP)

a/ Với m=2, phương trình thành: 2$x^{2}$+3x+1=0
=> x= -1/2 hoặc x= -1
b/ Để phương trình có nghiệm: $\Delta\geq$0
=> $(m+1)^{2}$- 4.m.1 $\geq$0 => $m^{2}- 2m+1\geq$0 (luôn đúng)
Vậy với mọi m thì phương trình luôn có nghiệm 

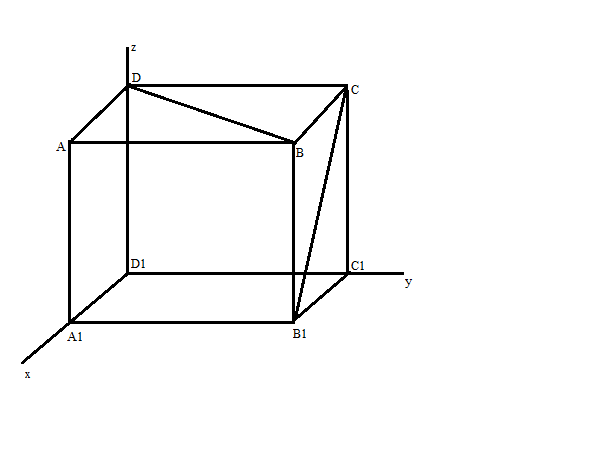Gắn hệ trục tọa độ vào hình vẽ sao cho $D_{1}$ trùng với gốc tọa độ O, $D_{1}A_{1}$ trùng với Ox, $D_{1}C_{1}$ trùng với Oy, $D_{1}D_{}$ trùng với Oz
Khi đó tọa độ các điểm là: D(0,0,a), B(a,a,a), C(0,a,a), $B_{1}$(a,a,0)
=> Khoảng cách giữa BD và $CB_{1}$ là: h= $\frac{\left| {\left[ {\overrightarrow{BD},\overrightarrow{CB_{1}}} \right].\overrightarrow{CD}} \right|}{\left| {\left[ {\overrightarrow{BD},\overrightarrow{CB_{1}}} \right]} \right|}$ = $\frac{a}{\sqrt{3}}$

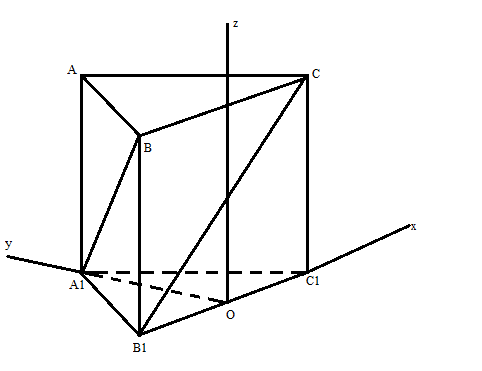Gắn hệ trục tọa độ vào trong hình vẽ sao cho trung điểm O của $B_{1}C_{1}$ chính là gốc tọa độ, $OC_{1}$ trùng với Ox, $OA_{1}$ trùng với Oy, Oz vuông góc với mp ($A_{1}B_{1}C_{1}$) và cùng chiều với hình chóp
Khi đó tọa độ các điểm là: C(a/2, 0,a), B1(-a/2,0,0), B(-a/2,0 ,a), A1(0,$\frac{a\sqrt{3}}{2}$,0)
Khi đó, khoảng cách giưã $CB_{1}$ và $BA_{1}$ là: h= $\frac{\left| {\left[ {\overrightarrow{BA_{1}},\overrightarrow{CB_{1}}} \right]. \overrightarrow{BC}} \right|}{\left| {\left[ {\overrightarrow{CB_{1}},\overrightarrow{BA_{1}}} \right]} \right|}$ = $\frac{3a}{\sqrt{66}}$

Chọn ngẫu nhiên 3 viên mà có cả bi đỏ và bi xanh có số cách là: 
+/ 1 đỏ, 1 xanh, 1 vàng: $C^{1}_{6}.C^{1}_{5}.C^{1}_{4}$ = 120
+/ 1 đỏ, 2 xanh:  $C^{1}_{6}.C^{2}_{5}$= 60
+/ 2 đỏ, 1 xanh:  $C^{2}_{6}.C^{1}_{5}$= 75
=> Có tổng số cách chọn thỏa mãn là: 120+60+75 =255 

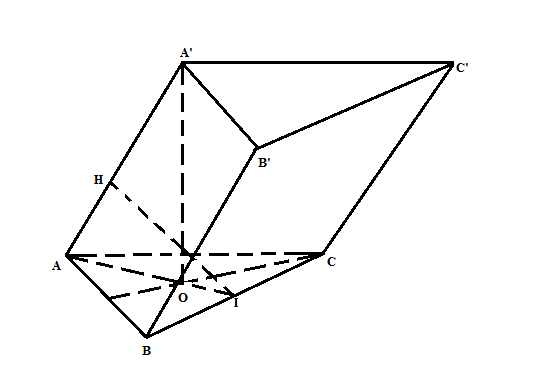Gọi I là trung điểm của BC
Trong mp(A'AI) kẻ IH vuông góc với AA' (H$\in$AA')
Ta có: BC vuông góc với AI, BC vuông góc với A'O => BC vuông góc với (A'AI) => BC vuông góc với IH
=> IH là đường vuông góc chung của BC và AA' => IH= $\frac{a\sqrt{3}}{8}$ 
Có AI là trung tuyến trong $\Delta$ABC đều cạnh a => AI= $\frac{a\sqrt{3}}{2}$ 
Xét $\Delta$AHI vuông tại H => sin HAI= HI/ AI => 1/4
Xét $\Delta A'OA$ vuông tại O  => A'O= OA. tan HAI= $\frac{a\sqrt{3}}{3}$. $\frac{1}{\sqrt{15}}$ = $\frac{a}{3\sqrt{5}}$
=> $V_{lăng trụ}$ =  A'O. $S_{ABC}$= $\frac{a}{3\sqrt{5}}$. $\frac{a^{2}.\sqrt{3}}{4}$= $\frac{a^{3}.\sqrt{15}}{60}$