|
|
giải đáp
|
hình giải tích
|
|
|
|
A thuộc AD và AH => A(3, -5)
BC qua C(-3,1) và vuông góc với AH => phương trình BC:7x-y+22=0 => B(x0,7x0+22)
AC−→−=(-6,6)=(-1,1) => phương trình AC: x+y+2=0
Lấy K đối xứng với B qua AD (K$\in $AC) => BK qua B và vuông góc với AD => phương trình BK: 3x-y+4$x_{0}$+22=0
=>K($x_{1}$, $y_{1}$=$3x_{1}$+4$x_{0}$+22)
Mặt khác, K$\in $AC nên tọa độ K thỏa mãn: 4$x_{1}$+4$x_{0}$+22=0 => $x_{1}$= $\frac{11-2x_{0}}{2}$
=> K($\frac{11-2x_{0}}{2}$, $x_{0}$+$\frac{77}{2}$)
Khi đó, $\overrightarrow{AB}$ ($x_{0}$-3, 7$x_{0}$+27) =>AB=$\sqrt{(x_{0}-3)^{2}+(7x_{0}+27)^{2}}$
$\overrightarrow{AK}$(5/2-$x_{0}$,$x_{0}$+87/2) =>AK= $\sqrt{(5/2-x_{0})^{2}+(x_{0}+87/2)^{2}}$
Giaỉ phương trình AK= AB, ta được hoặc $x_{0}$= 11/4 =>B(11/4, 165/4)
hoặc $x_{0}$= -211/24 =>B( -211/24, -949/24)
Cả 2 trường hợp này đều thỏa mãn, từ tọa đừ tọa độ A,B,C vừa tìm được ta viết được phương trình các cạnh trong tam giác ABC!
|
|
|
|
giải đáp
|
hình giải tích
|
|
|
|
A thuộc AD và AH => A(3, -5)
BC qua C(-3,1) và vuông góc với AH => phương trình BC:7x-y+22=0 => B(x0,7x0+22)
AC−→−=(-6,6)=(-1,1) => phương trình AC: x+y+2=0
Lấy K đối xứng với B qua AD (K$\in $AC) => BK qua B và vuông góc với AD => phương trình BK: 3x-y+4$x_{0}$+22=0
=>K($x_{1}$, $y_{1}$=$3x_{1}$+4$x_{0}$+22)
Mặt khác, K$\in $AC nên tọa độ K thỏa mãn: 4$x_{1}$+4$x_{0}$+22=0 => $x_{1}$= $\frac{11-2x_{0}}{2}$
=> K($\frac{11-2x_{0}}{2}$, $x_{0}$+$\frac{77}{2}$)
Khi đó, $\overrightarrow{AB}$ ($x_{0}$-3, 7$x_{0}$+27) =>AB=$\sqrt{(x_{0}-3)^{2}+(7x_{0}+27)^{2}}$
$\overrightarrow{AK}$(5/2-$x_{0}$,$x_{0}$+87/2) =>AK= $\sqrt{(5/2-x_{0})^{2}+(x_{0}+87/2)^{2}}$
Giaỉ phương trình AK= AB, ta được hoặc $x_{0}$= 11/4 =>B(11/4, 165/4)
hoặc $x_{0}$= -211/24 =>B( -211/24, -949/24)
Cả 2 trường hợp này đều thỏa mãn, từ tọa đừ tọa độ A,B,C vừa tìm được ta viết được phương trình các cạnh trong tam giác ABC!
|
|
|
|
bình luận
|
hình giải tích
:) Hình như mọi người không đọc thì phải ah, đây là một lời giải sai vì nhầm đề bài! Vậy mà mình vẫn được vote up!
|
|
|
|
|
|
|
|
|
|
sửa đổi
|
hình giải tích
|
|
|
|
A thuộc AD và AH => A(3, -5)BC qua C(-3,1) và vuông góc với AH => phương trình BC:7x-y+22=0 => B($x_{0}$,7$x_{0}$+22)D là trung điểm của BC => D($\frac{x_{0}-3}{2}$,$\frac{7x_{0}+23}{2}$). Mà D$\in $AD nên tọa độ D thỏa mãn phương trình: $\frac{x_{0}-3}{2}$+$\frac{7(7x_{0}+23)}{2}$+32=0 => $x_{0}$=$\frac{-111}{25}$=> B($\frac{-111}{25}$,$\frac{-227}{25}$)Khi đó: $\overrightarrow{AB}$=($\frac{-186}{25}$,$\frac{-102}{25}$)=(31,17) => phươg ntrình AB: 17x-31y-206=0$\overrightarrow{AC}$=(-6,6)=(-1,1) => phuuwo ngtrình AC: x+y+2=0$\overrightarrow{BC}$=($\frac{36}{25}$,$\frac{252}{25}$)=(1,7) => phươg ntrình BC : 7x-y-26=0
A thuộc AD và AH => A(3, -5)BC qua C(-3,1) và vuông góc với AH => phương trình BC:7x-y+22=0 => B($x_{0}$,7$x_{0}$+22)D là trung điểm của BC => D($\frac{x_{0}-3}{2}$,$\frac{7x_{0}+23}{2}$). Mà D$\in $AD nên tọa độ D thỏa mãn phương trình: $\frac{x_{0}-3}{2}$+$\frac{7(7x_{0}+23)}{2}$+32=0 => $x_{0}$=$\frac{-111}{25}$=> B($\frac{-111}{25}$,$\frac{-227}{25}$)Khi đó: $\overrightarrow{AB}$=($\frac{-186}{25}$,$\frac{-102}{25}$)=(31,17) => phương trình AB: 17x-31y-206=0$\overrightarrow{AC}$=(-6,6)=(-1,1) => phương trình AC: x+y+2=0$\overrightarrow{BC}$=($\frac{36}{25}$,$\frac{252}{25}$)=(1,7) => phươngtrình BC : 7x-y-26=0
|
|
|
|
giải đáp
|
hình giải tích
|
|
|
|
A thuộc AD và AH => A(3, -5)
BC qua C(-3,1) và vuông góc với AH => phương trình BC:7x-y+22=0 => B($x_{0}$,7$x_{0}$+22)
D là trung điểm của BC => D($\frac{x_{0}-3}{2}$,$\frac{7x_{0}+23}{2}$). Mà D$\in $AD nên tọa độ D thỏa mãn phương trình: $\frac{x_{0}-3}{2}$+$\frac{7(7x_{0}+23)}{2}$+32=0 => $x_{0}$=$\frac{-111}{25}$
=> B($\frac{-111}{25}$,$\frac{-227}{25}$)
Khi đó: $\overrightarrow{AB}$=($\frac{-186}{25}$,$\frac{-102}{25}$)=(31,17) => phương trình AB: 17x-31y-206=0
$\overrightarrow{AC}$=(-6,6)=(-1,1) => phương trình AC: x+y+2=0
$\overrightarrow{BC}$=($\frac{36}{25}$,$\frac{252}{25}$)=(1,7) => phươngtrình BC : 7x-y-26=0
|
|
|
|
giải đáp
|
phương trình đường thẳng
|
|
|
|
BC qua B(-4,0) và vuông góc với AH => BC: 3x+4y+12=0 => C(0,-3)
A $\in $AH =>A($x_{0}$, $y_{0}$=$\frac{4x_{0}-2}{3}$)
M là trung điểm AB => M($\frac{x_{0}-4}{2}$;$\frac{2x_{0}-1}{3}$)
Mặt khác, M$\in $CM => Tọa độ M thỏa mãn phương trình: 2($x_{0}$-4)+$\frac{2x_{0}-1}{3}$+3=0 => $x_{0}$=2
=> A(2,2)
Khi đó, $\overrightarrow{AB}$(-6,-2)=(3,1) => phương trình AB: x-3y+4=0
$\overrightarrow{AC}$(-2,-5)=(2,5) => phương trình AC: 5x-2y+20=0
$\overrightarrow{BC}$(4,-3) => phương trình BC: 3x+4y+12=0
|
|
|
|
sửa đổi
|
Tìm tâm bán kính mặt cầu ?
|
|
|
|
Gắn hệ trục tọa độ vào hình vẽ sao cho C trùng O (0,0,0), CA trùng Ox, CB trùng Oy. Từ C kẻ Cz song song SI => Cz vuông góc với mp (ABC)Khi đó: C(0,0,0), A(a$\sqrt{2}$,0,0), B(0,a$\sqrt{2}$,0) (Do $\Delta$ABC là tam giác vuông tại C => AB=AC$\sqrt{2}$ => AC= a$\sqrt{2}$)$\Delta$ABC là tam giác vuông cân tại C, H là trung diểm AB => CH vuông góc với ABTrong mp (ABC) , kẻ IN vuông góc với CBXét $\Delta$CNI đồng dạng $\Delta$CHB=> $\frac{IN}{BH}$=$\frac{CI}{CB}$=> IN=$\frac{a}{2\sqrt{2}}$ (BH=1/2AB; CI=1/2CH=1/4AB=a/2)I cách đều AB, AC=> IA=IB=> I($\frac{a}{2\sqrt{2}}$,$\frac{a}{2\sqrt{2}}$,0)=> S($\frac{a}{2\sqrt{2}}$,$\frac{a}{2\sqrt{2}}$,$\frac{a}{2}$)Gọi G(x,y,z) là tâmamặt cầu S.ABI => GA=GB=GC=GSGiaỉ hệ 3 phươ trngình 3 ẩn được tọa độ G($\frac{-3a}{4\sqrt{2}}$,$\frac{-3a}{4\sqrt{2}}$,$\frac{-3a}{4}$)Từ đó, bán kính mặt cầu S.ABI là R=GA= $\frac{a\sqrt{13}}{2\sqrt{2}}$
Gắn hệ trục tọa độ vào hình vẽ sao cho C trùng O (0,0,0), CA trùng Ox, CB trùng Oy. Từ C kẻ Cz song song SI => Cz vuông góc với mp (ABC)Khi đó: C(0,0,0), A(a$\sqrt{2}$,0,0), B(0,a$\sqrt{2}$,0) (Do $\Delta$ABC là tam giác vuông tại C => AB=AC$\sqrt{2}$ => AC= a$\sqrt{2}$)$\Delta$ABC là tam giác vuông cân tại C, H là trung diểm AB => CH vuông góc với ABTrong mp (ABC) , kẻ IN vuông góc với CBXét $\Delta$CNI đồng dạng $\Delta$CHB=> $\frac{IN}{BH}$=$\frac{CI}{CB}$=> IN=$\frac{a}{2\sqrt{2}}$ (BH=1/2AB; CI=1/2CH=1/4AB=a/2)I cách đều AB, AC=> IA=IB=> I($\frac{a}{2\sqrt{2}}$,$\frac{a}{2\sqrt{2}}$,0)=> S($\frac{a}{2\sqrt{2}}$,$\frac{a}{2\sqrt{2}}$,$\frac{a}{2}$)Gọi G(x,y,z) là tâm mặt cầu S.ABI => GA=GB=GC=GSGiải hệ 3 phương trình 3 ẩn được tọa độ G($\frac{-3a}{4\sqrt{2}}$,$\frac{-3a}{4\sqrt{2}}$,$\frac{-3a}{4}$)Từ đó, bán kính mặt cầu S.ABI là R=GA= $\frac{a\sqrt{13}}{2\sqrt{2}}$
|
|
|
|
sửa đổi
|
Tìm tâm bán kính mặt cầu ?
|
|
|
|
Gắn hệ trục tọa độ vào hình vẽ sao cho C trùng O (0,0,0), CA trùng Ox, CB trùng Oy. Từ C kẻ Cz song song SI => Cz vuông góc với mp (ABC)Khi đó: C(0,0,0), A(a$\sqrt{2}$,0,0), B(0,a$\sqrt{2}$,0) (Do $\Delta$ABC là tam giác vuông tại C => AB=AC$\sqrt{2}$ => AC= a$\sqrt{2}$)$\Delta$ABC là tam giác vuông cân tại C, H là trung diểm AB => CH vuông góc với ABTrong mp (ABC) , kẻ IN vuông góc với CBXét $\Delta$CNI đồng dạng $\Delta$CHB=> $\frac{IN}{BH}$=$\frac{CI}{CB}$=> IN=$\frac{a}{2\sqrt{2}}$ (BH=1/2AB; CI=1/2CH=1/4AB=a/2)I cách đều AB, AC=> IA=IB=> I($\frac{a}{2\sqrt{2}}$,$\frac{a}{2\sqrt{2}}$,0)=> S($\frac{a}{2\sqrt{2}}$,$\frac{a}{2\sqrt{2}}$,$\frac{a}{2}$)Gọi G(x,y,z) là tâmamặt cầu S.ABI => GA=GB=GC=GSGiaỉ hệ 3 phươ trngình 3 ẩn được tọa độ G($\frac{-3a}{4\sqrt{2}}$,$\frac{-3a}{4\sqrt{2}}$,$\frac{-3a}{4}$)Từ đó, bán kính mặt cầu S.ABI là R=GA= $\frac{a\sqrt{13}}{2\sqrt{2}}$
Gắn hệ trục tọa độ vào hình vẽ sao cho C trùng O (0,0,0), CA trùng Ox, CB trùng Oy. Từ C kẻ Cz song song SI => Cz vuông góc với mp (ABC)Khi đó: C(0,0,0), A(a$\sqrt{2}$,0,0), B(0,a$\sqrt{2}$,0) (Do $\Delta$ABC là tam giác vuông tại C => AB=AC$\sqrt{2}$ => AC= a$\sqrt{2}$)$\Delta$ABC là tam giác vuông cân tại C, H là trung diểm AB => CH vuông góc với ABTrong mp (ABC) , kẻ IN vuông góc với CBXét $\Delta$CNI đồng dạng $\Delta$CHB=> $\frac{IN}{BH}$=$\frac{CI}{CB}$=> IN=$\frac{a}{2\sqrt{2}}$ (BH=1/2AB; CI=1/2CH=1/4AB=a/2)I cách đều AB, AC=> IA=IB=> I($\frac{a}{2\sqrt{2}}$,$\frac{a}{2\sqrt{2}}$,0)=> S($\frac{a}{2\sqrt{2}}$,$\frac{a}{2\sqrt{2}}$,$\frac{a}{2}$)Gọi G(x,y,z) là tâmamặt cầu S.ABI => GA=GB=GC=GSGiaỉ hệ 3 phươ trngình 3 ẩn được tọa độ G($\frac{-3a}{4\sqrt{2}}$,$\frac{-3a}{4\sqrt{2}}$,$\frac{-3a}{4}$)Từ đó, bán kính mặt cầu S.ABI là R=GA= $\frac{a\sqrt{13}}{2\sqrt{2}}$
|
|
|
|
giải đáp
|
Tìm tâm bán kính mặt cầu ?
|
|
|
|
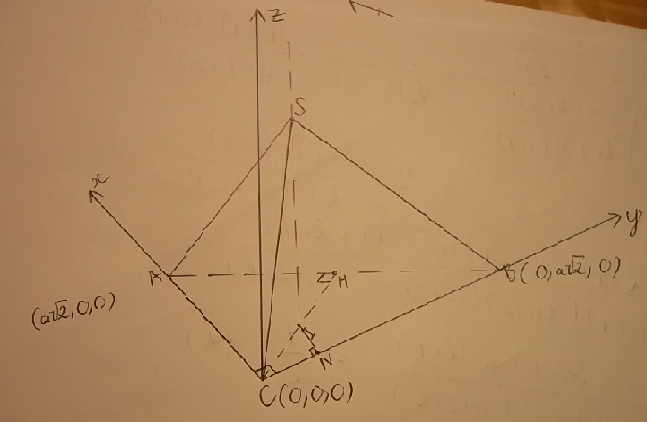 Gắn hệ trục tọa độ vào hình vẽ sao cho C trùng O (0,0,0), CA trùng Ox, CB trùng Oy. Từ C kẻ Cz song song SI => Cz vuông góc với mp (ABC) Khi đó: C(0,0,0), A(a$\sqrt{2}$,0,0), B(0,a$\sqrt{2}$,0) (Do $\Delta$ABC là tam giác vuông tại C => AB=AC$\sqrt{2}$ => AC= a$\sqrt{2}$) $\Delta$ABC là tam giác vuông cân tại C, H là trung diểm AB => CH vuông góc với AB Trong mp (ABC) , kẻ IN vuông góc với CB Xét $\Delta$CNI đồng dạng $\Delta$CHB => $\frac{IN}{BH}$=$\frac{CI}{CB}$=> IN=$\frac{a}{2\sqrt{2}}$ (BH=1/2AB; CI=1/2CH=1/4AB=a/2) I cách đều AB, AC=> IA=IB=> I($\frac{a}{2\sqrt{2}}$,$\frac{a}{2\sqrt{2}}$,0) => S($\frac{a}{2\sqrt{2}}$,$\frac{a}{2\sqrt{2}}$,$\frac{a}{2}$) Gọi G(x,y,z) là tâm mặt cầu S.ABI => GA=GB=GC=GS Giải hệ 3 phương trình 3 ẩn được tọa độ G($\frac{-3a}{4\sqrt{2}}$,$\frac{-3a}{4\sqrt{2}}$,$\frac{-3a}{4}$) Từ đó, bán kính mặt cầu S.ABI là R=GA= $\frac{a\sqrt{13}}{2\sqrt{2}}$ |
|
|
|
|
|
bình luận
|
Hàm biến phức!
Mình cũng thấy ở đây chủ yếu là toán cấp 3, nhưng cũng chưa thấy có thông báo chính thức gì về giới hạn nội dung. Nếu nó không phù hợp thì admin xóa giúp với ạ! Thank a lot
|
|
|
|
|
|
|
|
đặt câu hỏi
|
Hàm biến phức!
|
|
|
|
Hãy xây dựng một ví dụ chỉ ra rằng hệ Cauchy- Riemann thỏa mãn 2 hàm u( x, y), v(x,y) tại một điểm ($x_{0}, y_{0}$) nhưng hàm số: f(z) = u(x,y)+ iv(x,y) không có đạo hàm tại $z_{0} = x_{0}+ y_{0}$
|
|
|
|
bình luận
|
giúp mình bài này nhé
Sao bài này lại thuộc tính đơn điệu của hàm số, sắp xếp lộn xộn thế này sẽ rất khó cho người tìm kiếm về sau!
|
|
|
|
|
|
|
|
sửa đổi
|
giúp mình bài này nhé
|
|
|
|
(SAB), (SAD) vuông góc với (ABCD)=> SA vuông góc với (ABCD)Khi đó ta đồng nhất được hệ trục tọa độ với hình sao cho A trùng O, AB trùng Ox, AD trùng Oy, AS trùng Oz=> A( 0,0,0), B(a, 0, 0), C (a, a,0), D( 0,a,0), S(0,0,a)$\overrightarrow{SD}$= (0,a,-a), $\overrightarrow{SC}$=(a, a, -a) =>
$\left[ {\overrightarrow{SD}\times \overrightarrow{SC}} \right]$= (0,
-$a^{2}$, -$a^{2}$)= (0,1,1) => phương trình mp(SDC): y+ z=0$\overrightarrow{AB}$= (a,0,0), $\overrightarrow{DA}$=(0, a, 0) =>
$\left[ {\overrightarrow{AB}\times \overrightarrow{DA}} \right]$= (
-a, -a, $a^{2}$)= (-1, -1,a) => phương trình mp(ABCD): -x-y+ az=0$\overrightarrow{AS}$= (0,0,a), $\overrightarrow{AD}$=(0, a,0) =>
$\left[ {\overrightarrow{ÁS}\times \overrightarrow{AD}} \right]$= (
-$a^{2}$, a, 0)= (-a,1,0) => phương trình mp(SAD): -ax+y=0$\overrightarrow{AS}$= (0,0,a), $\overrightarrow{AB}$=(a, 0,0) =>
$\left[ {\overrightarrow{AS}\times \overrightarrow{AB}} \right]$= (-a, $a^{2}$, -a)= (-1,a, -1) => phương trình mp(SAB): -x+ay- z=0$\overrightarrow{SB}$= (a,0,-a), $\overrightarrow{SC}$=(a, a, -a) =>
$\left[ {\overrightarrow{SB}\times \overrightarrow{SC}} \right]$= (a^2, 0, $a^{2}$)= (1,0,1) => phương trình mp(SBC): y+ z-a=0Gọi I( $x_{0}$, $y_{0}$, $z_{0}$) là tâm hình cầu nội tiếp hình chópKhoảng cách d(I, (SDC)) = $\frac{y_{0}+z_{0}}{\sqrt{2}}$Khoảng cách d(I, (ABCD))=$\frac{-x_{0}-y_{0}+az_{0}}{\sqrt{2+a^{2}}}$Khoảng cách d( I, (SAD))= $\frac{-ax_{0}+y_{0}}{\sqrt{a^{2}+1}}$Khoảng cách d(I, ( SAB))= $\frac{-x_{0}+ay_{0}-z_{0}}{\sqrt{a^{2}+2}}$Khoảng cách d(I, (SBC))= $\frac{x_{0}+z_{0}-a}{\sqrt{a^{2}+2}}$Xét d(I, (SAB))= d(I, (ABCD))=> -$y_{0}+az_{0}= ay_{0}- z_{0}$=> $ay_{0}-az_{0}= z_{0}-y_{0}$=> a($y_{0}-z_{0)= z_{0}-y_{0}}$=> a= (-1)Thay a=(-1), xét d(I, (SDC))= d(I, (SAD))=> $\frac{y_{0}+z_{0}}{\sqrt{2}}$= $\frac{x_{0}+y_{0}}{\sqrt{2}}$=> $x_{0}=z_{0}$Thay a=(-1), $x_{0}=z_{0}$, xét d(I, (SBC))= d( I, (SAB))=> 4$x_{0}+y_{0}+1$=0Thay các kết quả tìm được ở trên, xét d( I, (SDC))= d( I, (SAB))=> $\frac{-1-3x_{0}}{\sqrt{2}=\frac{2x_{0}+1}{\sqrt{3}}}$=> $x_{0}$= -1Từ đó suy ra: $y_{0}=3; z_{0}= -1$Vậy bán kính hình cầu nội tiếp hình chóp là: R= d (I, (SDC))= \frac{y_{0}+z_{0}}{\sqrt{2}} = $\frac{3+ (-1)}{\sqrt{2}}$= $\sqrt{2}$
(SAB), (SAD) vuông góc với (ABCD)=> SA vuông góc với (ABCD)Khi đó ta đồng nhất được hệ trục tọa độ với hình sao cho A trùng O, AB trùng Ox, AD trùng Oy, AS trùng Oz=> A( 0,0,0), B(a, 0, 0), C (a, a,0), D( 0,a,0), S(0,0,a)$\overrightarrow{SD}$= (0,a,-a), $\overrightarrow{SC}$=(a, a, -a) =>
$\left[ {\overrightarrow{SD}\times \overrightarrow{SC}} \right]$= (0,
-$a^{2}$, -$a^{2}$)= (0,1,1) => phương trình mp(SDC): y+ z=0$\overrightarrow{AB}$= (a,0,0), $\overrightarrow{DA}$=(0, a, 0) =>
$\left[ {\overrightarrow{AB}\times \overrightarrow{DA}} \right]$= (
-a, -a, $a^{2}$)= (-1, -1,a) => phương trình mp(ABCD): -x-y+ az=0$\overrightarrow{AS}$= (0,0,a), $\overrightarrow{AD}$=(0, a,0) =>
$\left[ {\overrightarrow{ÁS}\times \overrightarrow{AD}} \right]$= (
-$a^{2}$, a, 0)= (-a,1,0) => phương trình mp(SAD): -ax+y=0$\overrightarrow{AS}$= (0,0,a), $\overrightarrow{AB}$=(a, 0,0) =>
$\left[ {\overrightarrow{AS}\times \overrightarrow{AB}} \right]$= (-a, $a^{2}$, -a)= (-1,a, -1) => phương trình mp(SAB): -x+ay- z=0$\overrightarrow{SB}$= (a,0,-a), $\overrightarrow{SC}$=(a, a, -a) =>
$\left[ {\overrightarrow{SB}\times \overrightarrow{SC}} \right]$= (a^2, 0, $a^{2}$)= (1,0,1) => phương trình mp(SBC): y+ z-a=0Gọi I( $x_{0}$, $y_{0}$, $z_{0}$) là tâm hình cầu nội tiếp hình chópKhoảng cách d(I, (SDC)) = $\frac{y_{0}+z_{0}}{\sqrt{2}}$Khoảng cách d(I, (ABCD))=$\frac{-x_{0}-y_{0}+az_{0}}{\sqrt{2+a^{2}}}$Khoảng cách d( I, (SAD))= $\frac{-ax_{0}+y_{0}}{\sqrt{a^{2}+1}}$Khoảng cách d(I, ( SAB))= $\frac{-x_{0}+ay_{0}-z_{0}}{\sqrt{a^{2}+2}}$Khoảng cách d(I, (SBC))= $\frac{x_{0}+z_{0}-a}{\sqrt{a^{2}+2}}$Xét d(I, (SAB))= d(I, (ABCD))=> -$y_{0}+az_{0}= ay_{0}- z_{0}$=> $ay_{0}-az_{0}= z_{0}-y_{0}$=> a($y_{0}-z_{0)= z_{0}-y_{0}}$=> a= (-1)Thay a=(-1), xét d(I, (SDC))= d(I, (SAD))=> $\frac{y_{0}+z_{0}}{\sqrt{2}}$= $\frac{x_{0}+y_{0}}{\sqrt{2}}$=> $x_{0}=z_{0}$Thay a=(-1), $x_{0}=z_{0}$, xét d(I, (SBC))= d( I, (SAB))=> 4$x_{0}+y_{0}+1$=0Thay các kết quả tìm được ở trên, xét d( I, (SDC))= d( I, (SAB))=> $\frac{-1-3x_{0}}{\sqrt{2}}$= $\frac{2x_{0}+1}{\sqrt{3}}$=> $x_{0}$= -1Từ đó suy ra: $y_{0}=3; z_{0}= -1$Vậy bán kính hình cầu nội tiếp hình chóp là: R= d (I, (SDC))= \frac{y_{0}+z_{0}}{\sqrt{2}} = $\frac{3+ (-1)}{\sqrt{2}}$= $\sqrt{2}$
|
|