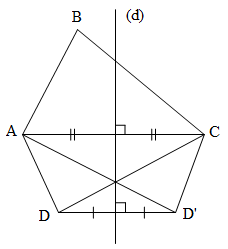
Gọi $d$ là đường trung trực của đoạn $AC$.
Xét phép đối xứng trục $(d)$
$S_{(d)}: D \rightarrow D'$
Ta có: $AD=CD', CD=AD'$ và $\Delta ADC=\Delta AD'C$
Suy ra $S_{ABCD}=S_{ABCD'}=S_{BAD'}+S_{BCD'}$.
$\Rightarrow
S_{ABCD}=\frac{1}{2}AB.AD'.\sin \widehat{BAD'}+\frac{1}{2}BC.CD'.\sin
\widehat{BCD'} \leq \frac{1}{2}(AB.AD'+BC.CD')$
$=\frac{1}{2} (AB.CD+BC.AD) $
Dấu "=" xảy ra khi ta có:
$\sin \widehat{BAD'}=\sin \widehat{BCD'}=1 \Rightarrow \widehat{BAD'}=\widehat{BCD'}=90^\circ $
$\Rightarrow ABCD'$ nội tiếp trong đường tròn đường kính $BD'$.
Suy ra $\widehat{ABC}+\widehat{ADC}=180^
\circ $
Do đó tứ giác $ABCD$ nội tiếp trong đường tròn đường kính $BD'$.
Suy ra $\widehat{BDD'}=90^
\circ $, tức là $BD \bot DD' \Rightarrow AC \bot BD$ do ($AC\parallel DD'$)
Đảo lại: Nếu $ABCD$ nội tiếp trong đường tròn $(O)$ với hai đường chéo $AC \bot BD$, vì $\widehat{BDD'}=90^
\circ $ nên dễ thấy $BD'$ là một đường kính của $(O)$. Từ đó suy ra $\widehat{D'AB}=\widehat{D'CB}=90^
\circ . $
Nên dấu
"=" xảy ra. Vậy $S_{ABCD} \leq \frac{1}{2}(AB.CD+BC.AD) $
Dấu
"=" xảy ra $\Leftrightarrow ABCD$ nội tiếp được và có hai đường chéo vuông góc với nhau.