|
|
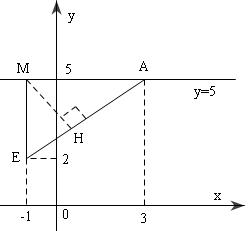
Phương trình ($C$): ${\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} = 9 \Rightarrow E( - 1;2),\,R = 3$
Dễ
thấy đường thẳng $x = 3$ qua $A(3;5)$ và không tiếp xúc với ($C$). Do
đó chỉ cần xét các đường thẳng qua $A$ và không song song với $Oy$,
đường thẳng qua $A$, hệ số góc $k$ có phương trình $y = k(x-3) + 5 $
$ \Leftrightarrow kx - y - 3k + 5 = 0$
Đường thẳng này là tiếp tuyến của ($C)\Leftrightarrow $khoảng cách từ $E$ đến đường thẳng $= R.$
$
\Leftrightarrow \frac{{| - k - 2 - 3k + 5|}}{{\sqrt {{k^2} + 1} }} = 3
\Leftrightarrow (3-4k)^2=9(k^2+1)\Leftrightarrow \left[
\begin{array}{l}
k = 0\\
k = \frac{{24}}{7}
\end{array} \right.$
Vậy qua A kẻ được tới đường tròn $2$ tiếp tuyến, phương trình của chúng là:
$y = 5;y = \frac{{24}}{7}(x - 3) + 5 = \frac{{24}}{7}x - \frac{{37}}{7}$
Gọi $M$ là tiếp điểm của đường thẳng $y = 5$ với ($C$) thì $\Delta AME$ vuông ở $M$ và có $EM = 3, AM = 4$
$\begin{array}{l}
\Rightarrow AE = 5\\
\Rightarrow MH = \frac{{EM.AM}}{{AE}} = \frac{{12}}{5}
\end{array}$
($MH$ là đường cao $\Delta AME$ $ \Rightarrow MH = \frac{1}{2}MN)$
$ \Rightarrow MN = 2MH = \frac{{24}}{5}$
|