|
|
Ta có :
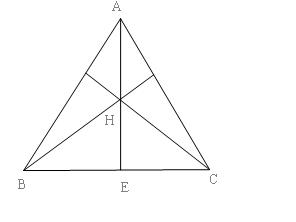
Vì $AE = 2HE \Rightarrow tanBtanC = 2 (1)$
Lại có $tanA - tan(B + C) = \frac{{tanB + tanC}}{{tanBtanC - 1}} (2)$
Từ $(1)(2)$ có $tanA=tanB+tanC (3)$
Từ $tanBtanC=2 \Rightarrow tanB,tanC$ cùng dấu $\Rightarrow tanB > 0,tanC > 0$ (do chúng không thể cùng âm)
Theo bất đẳng thức CÔSI, từ $(3)$ ta có : $tanA \ge 2\sqrt {tanBtanC} $
$ \Rightarrow tanA \ge 2\sqrt 2 \Rightarrow dpcm$
Nhận
xét:Ta có bài toán tổng quát sau: Cho tam giác $ABC$ nhọn, biết trực
tâm $H$ chia đường cao AE thoe tỉ số (tức $\frac{{AH}}{{HE}} = m$)
CMR: $tanA \ge 2\sqrt {m + 1} $
Cách giả bài toán tương tự như trên sau khi tính được $tanBtanC=m+1$
|