|
|
Theo định lý hàm số sin ,ta có:
a=b(1+2cos2B)⇔sinA=sinB(1+2cos2B)⇔sinA=sinB+sin3B−sinB⇔sinA=sin3B(1)
Từ (1) suy ra có 2 khả năng sau:
1. A=3B
Do mà A=3B nên
Dễ thấy :
Vậy AMC cũng là tam giác cân
2. Nếu A+3B=1800
Khi đó ta có A+3B=A+B+C
⇒C=2B
Kẻ AE⊥BC.Gọi M là điểm đối xứng của B qua E suy ra ABM
Là tam giác cân
Ta có mà C=2B nên suy ra :
Ta có (đpcm)
Mệnh đề đảo nói chung không đúng
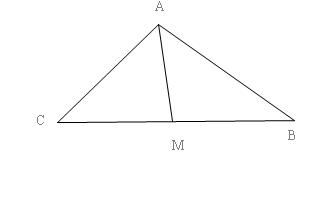
Xét tam giác ABC vuông tại A, C=700,B=200
Khi đó lấy M là trung điểm BC thì ta có
MB=MC=MA tức là tồn tại M sao cho ABM và ACM là tam giác cân
Nhưng khi đó sinA=1, sin3B=√32
⇒sinA≠sin3B⇒a≠b(1+2cosB)
Suy ra (đpcm)
|