|
|
1. Phép biến hình
ĐỊNH NGHĨA
Phép biến hình (trong mặt phẳng) là một quy tắc để với mỗi điểm M thuộc mặt phẳng, xác định được một điểm duy nhất M’ thuộc mặt phẳng ấy. Điểm M’ gọi là ảnh của điểm M qua phép biến hình đó.
2. Các ví dụ
Ví dụ 1
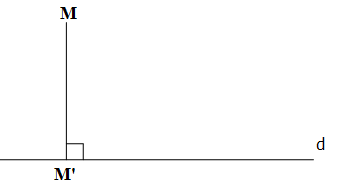
Cho đường thẳng d. Với mỗi điểm M, ta xác định M’ là hình chiếu (vuông góc) của M trên d thì ta được một phép biến hình.
Phép biến hình này gọi là phép chiếu (vuông góc) lên được thẳng d
Ví dụ 2
Cho vectơ $\overrightarrow u $, với mỗi điểm M ta xác định điểm M’ theo quy tắc $\overrightarrow {MM'} = \overrightarrow u $
Như vậy ta cũng có một phép biến hình. Phép biến hình đó gọi là phép tịnh tiến theo vectơ $\overrightarrow u $

3. Kí hiệu và thuật ngữ
Nếu ta kí hiệu một phép biến hình nào đó là F và điểm M’ là ảnh của điểm M qua phép biến hình F thì ta viết $M' = F\left( M \right)$, hoặc $F\left( M \right) = M'$. Khi đó ta còn nói phép biến hình F biến điểm M thành điểm M’
Với mỗi hình (H) ta gọi hình (H’) gồm các điểm $M' = F\left( M \right)$, trong đó $M \in (H)$là ảnh của (H) qua phép biến hình F, và viết $H' = F\left( H \right)$.
|