|
|
1. Định nghĩa phép tịnh tiến
Ta nhắc lại định nghĩa phép tịnh tiến:
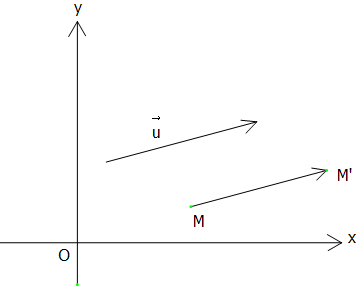
Phép tịnh tiến theo vectơ $\overrightarrow u $ là một phép biến hình biến điểm M thành điểm M’ sao cho$\overrightarrow {MM'} = \overrightarrow u $
Phép tịnh tiến theo vectơ $\overrightarrow u $ thường được kí hiệu là $T$ hoặc ${T_{\overrightarrow u }}$, vecto $\overrightarrow u $ được gọi là vectơ tịnh tiến
2. Các tính chất của phép tịnh tiến
ĐỊNH LÝ 1
Nếu phép tịnh tiến biến hai điểm M và N lần lượt thành hai điểm M’ và N’ thì $M’N’= MN$.
ĐỊNH LÝ 2
Phép tịnh tiến biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự ba điểm đó.
HỆ QUẢ
Phép tịnh tiến biến đường thẳng thành đường thẳng, biến tia thành tia, biến đoạn thẳng thành đoạn thẳng bằng nó, biến tam giác thành tam giác bằng nó, biến đường tròn thành đường tròn có cùng bán kính, biến góc thành góc bằng nó.
3. Biều thức tọa độ của phép tịnh tiến
Trong mặt phẳng với hệ trục tọa độ Oxy, cho phép tịnh tiến theo vectơ $\overrightarrow u $
Biết tọa độ của $\overrightarrow u $là (a ; b). Giả sử điểm M(x ; y) biến thành điểm M’(x’ ; y’)
Khi đó ta có $\left\{ \begin{array}{l}
x' = x + a\\
y' = y + b
\end{array} \right.$
4. Ứng dụng của phép tịnh tiến
Bài toán
Cho hai điểm B, C cố định trên đường tròn (O ; R) và một điểm A thay đổi trên đường tròn đó. Chứng minh rằng trực tâm tam giác ABC nằm trên một đường tròn cố định.
Giải
Nếu BC là đường kính thì trực tâm H của tam giác ABC chính là A. Vậy H nằm trên đường tròn cố định (O ; R).
Nếu BC không phải là đường kính, vẽ đường kính BB’ của đường tròn
Dễ thấy rằng nếu H là trực tâm của tam giác ABC thì $\overrightarrow {AH} = \overrightarrow {B'C} $ (trên hình 4, điều đó suy từ nhận xét tứ giác AHCB’ là hình bình hành).
Như vậy, phép tịnh tiến theo vectơ cố định $\overrightarrow {B'C} $ biến điểm A thành điểm H. Do đó, khi A thay đổi trên (O ; R) thì trực tâm H luôn nằm trên đường tròn cố định là ảnh của đường tròn (O ; R) qua phép tịnh tiến nói trên.
5. Phép dời hình
Không phải chỉ có phép tịnh tiến “không làm thay đổi khoảng cách giữa hai điểm” mà còn nhiều phép biến hình khác cũng có tính chất đo (tính chất này còn được gọi là tính chất bảo toàn khoảng cách giữa hai điểm). Người ta gọi các phép biến hình như vậy là phép dời hình.
ĐỊNH NGHĨA
Phép dời hình là phép biến hình không làm thay đổi khoảng cách giữa hai điểm bất kỳ.
ĐỊNH LÝ
Phép dời hình biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự ba điểm đó, biến đường thẳng thành đường thẳng, biến tia thành tia, biến đoạn thẳng thành đoạn thẳng bằng nó, biến tam giác thanh tam giac bằng nó, biến đường tròn thành đường tròn có cùng bán kính, biến góc thành góc bằng nó.
|