|
|
ĐỊNH LÝ
Giả sử hàm số f có đạo hàm trên khoảng I
a) Nếu $f'(x) > 0$ với mọi $x \in I$ thì hàm số f đồng biến trên khoảng I
b) Nếu $f'(x)<0$với mọi $x \in I$ thì hàm số f nghịch biến trên khoảng I
c) Nếu $f'(x) = 0$ với mọi $x \in I$ thì hàm số f không đổi trên khoảng I
CHÚ Ý
Khoảng I trong định lý trên có thể được thay bởi một đoạn hoặc một nửa khoảng, khi đó phải bổ sung giả thiết “hàm số liên tục trên đoạn nửa khoảng đó” chẳng hạn :
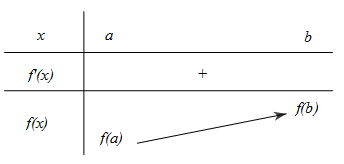
Nếu hàm số f liên tục trên đoạn [a;b] và có đạo hàm $f'(x) > 0$ trên khoảng (a;b) thì hàm số f đồng biến trên đoạn [a;b].
Người ta thường diễn đạt khẳng định này qua bảng biến thiên:
VÍ DỤ
Chứng minh rằng hàm số$f(x) = \sqrt {1 - {x^2}} $ nghịch biến trên đoạn [0 ; 1]
Giải
Dễ thấy hàm số đã cho liên tục đoạn [0 ; 1]. Ngoài ra, $f'(x) = \frac{{ - x}}{{\sqrt {1 - {x^2}} }} < 0$
với mọi $x \in (0;1)$ do đó hàm số nghịch biến trên đoạn [0 ; 1].
Việc tìm các khoảng đồng biến và nghịch biến của một hàm số còn được gọn là xét chiều biến thiên của hàm số đó.
Qua định lý đã nêu, ta thấy việc xét chiều biến thiên của một hàm số có đạo hàm có thể chuyển về việc xét dấu đạo hàm của nó.
Ví dụ: Xét chiều biến thiên của hàm số: $y = x + \frac{4}{x}$
Giải:
Hàm số đã cho xác định với mọi x khác 0
Ta có: $y' = 1 - \frac{4}{{{x^2}}} = \frac{{{x^2} - 4}}{{{x^2}}}$
$y' = 0 \Leftrightarrow x = \pm 2$
Chiều biến thiên của hàm số được nêu trong bảng:
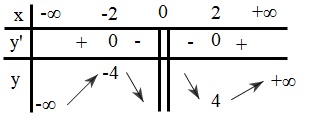
Vậy hàm số đồng biến trên mỗi khoảng $( - \infty ; - 2)\& (2; + \infty )$, nghịch biến trên mỗi khoảng $( - 2;0)\& (0;2)$
|