|
|
1. Nhắc lại về hàm số bậc nhất
Ta đã biết: Hàm số bậc nhất là hàm số được cho bằng biểu thức có dạng $y = ax + b$, trong đó a và b là những hằng số với $a \ne 0$.
Hàm số bậc nhất có tập xác định là R
Khi $a > 0$, hàm số $y = ax + b$ đồng biến trên R
Khi $a < 0$, hàm số $y = ax + b$ nghịch biến trên R
Bảng biến thiên:
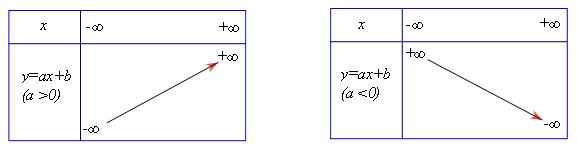
Đồ thị của hàm số $y = ax + b\,\,(a \ne 0)$ là 1 đường thẳng gọi là đường thẳng $y = ax + b$. Nó có hệ số góc bằng $a$ và có đặc điểm sau:
- Không song song và không trùng với các trục tọa độ
- Cắt trục tung tại điểm $B(0;b)$ và cắt trục hoành tại điểm $A( - \frac{b}{a};0)$
2. Hàm số $y = |{\text{ax}} + b|$
a, Hàm số bậc nhất trên từng khoảng
Xét hàm số $y = f(x) =\begin{cases}x + 1\,\,\,\,\,\,\,\,\,\,\,;\,0 \leqslant x < 2 \\- \frac{1}{2}x + 4\,\,\,;\,2 \leqslant x \leqslant 4 \\ 2x - 6\,\,\,\,\,\,\,\,\,;\,4 < x \leqslant 5 \end{cases} $
Đồ thị của hàm số trên:
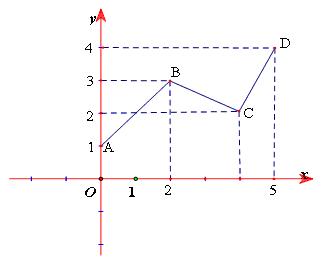
Rõ ràng, hàm số trên không phải là hàm số bậc nhất. Nó là sự “lắp ghép” của ba hàm số bậc nhất khác nhau. Hàm số này là một ví dụ về hàm số bậc nhất trên từng khoảng
Muốn vẽ đồ thị của hàm số bậc nhất trên từng khoảng, ta vẽ đồ thị của từng hàm số tạo thành. Chẳng hạn, đồ thị của hàm số nêu trên là đường gấp khúc ABCD, trong đó
AB là phần đường thẳng $y = x + 1$ ứng với $0 \leqslant x < 2$
BC là phần đường thẳng $y = - \frac{1}{2}x + 4$ ứng với $2 \leqslant x \leqslant 4$
CD là phần đường thẳng $y = 2x - 6$ ứng với $4 < x \leqslant 5$
b, Đồ thị và sự biến thiên của hàm số $y = |{\text{ax}} + b|$ với
Ví dụ: Xét hàm số $y = |2x - 4|$
Theo định nghĩa giá trị tuyệt đối ta có:
- Nếu $2x - 4 \geqslant 0$, tức là $x \geqslant 2$ thì $|2x - 4| = 2x - 4$
- Nếu $2x - 4 < 0$, tức là $x < 2$ thì $|2x - 4| = - (2x - 4) = - 2x + 4$
Do đó, hàm số đã cho có thể viết là
$y = \begin{cases}2x - 4,x \geqslant 2\\ - 2x + 4,x < 2 \end{cases} $
CHÚ Ý
Qua ví dụ trên, ta thấy có thể vẽ đồ thị của hàm số$y = |{\text{ax}} + b|$ bằng một cách khác đơn giản hơn như sau: Vẽ hai đường thẳng $y = {\text{ax}} + b$ và $y = - {\text{ax}} - b$ rồi xóa đi hai phần đường thẳng nằm ở phía dưới trục hoành.
|