|
|
Định lí và các quy tắc này được áp dụng cho mọi trường hợp : $x \to {x_0},\,x \to {x_0}^ + ,\,x \to {x_0}^ - ,\,x \to + \infty ,\,x \to - \infty $
ĐỊNH LÍ: Nếu $\mathop {\lim }\limits_{x \to {x_0}} \left| {f\left( x \right)} \right| = + \infty $ thì $\mathop {\lim }\limits_{x \to {x_0}} \frac{1}{{f\left( x \right)}} = 0$
Quy tắc 1: Nếu $\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = \pm \infty $ và $\mathop {\lim }\limits_{x \to {x_0}} g\left( x \right) = L \ne 0$ thì $\mathop {\lim }\limits_{x \to {x_0}} \left[ {f\left( x \right)g\left( x \right)} \right]$ được cho trong bảng sau:

Ví dụ 1: Tìm $\mathop {\lim }\limits_{x \to - \infty } \left( {2{x^3} - {x^2} + 3x - 5} \right)$
Ta có: $2{x^3} - {x^2} + 3x - 5 = {x^3}\left( {2 - \frac{1}{x} + \frac{3}{{{x^2}}} - \frac{5}{{{x^3}}}} \right)$ với mọi $x \ne 0$
Vì $\mathop {\lim }\limits_{x \to - \infty } {x^3} = - \infty $ và $\mathop {\lim }\limits_{x \to - \infty } \left( {2 - \frac{1}{x} + \frac{3}{{{x^2}}} - \frac{5}{{{x^3}}}} \right) = 2 > 0$ nên $\mathop {\lim }\limits_{x \to - \infty } \left( {2{x^3} - {x^2} + 3x - 5} \right) = - \infty $
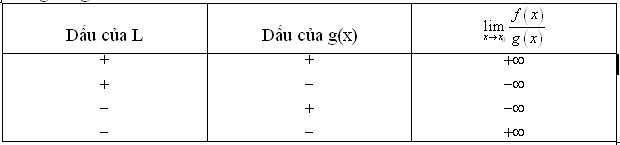
Quy tắc 2: Nếu $\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = L \ne 0,\,\,\mathop {\lim }\limits_{x \to {x_0}} g(x) = 0$ và và $g\left( x \right) > 0$ hoặc $g\left( x \right) < 0$ với mọi $x \in J\backslash \left\{ {{x_0}} \right\}$, trong đó J là một khoảng nào đó chứa ${x_0}$thì $\mathop {\lim }\limits_{x \to {x_0}} \frac{{f\left( x \right)}}{{g\left( x \right)}}$ được cho trong bảng sau:
Ví dụ: Tìm $\mathop {\lim }\limits_{x \to {1^ - }} f(x) = \mathop {\lim }\limits_{x \to {1^ - }} \sqrt {1 - {x^2}} = 0 = f\left( { - 1} \right)$$\mathop {\lim }\limits_{x \to - 2} \frac{{2x + 1}}{{{{\left( {x + 2} \right)}^2}}}$
Giải: Ta có $\mathop {\lim }\limits_{x \to - 2} (2x + 1) = - 3 < 0,\,\,\mathop {\lim }\limits_{x \to - 2} {(x + 2)^2} = 0;\,\,\,{\left( {x + 2} \right)^2} > 0$ với mọi $x \ne - 2$. Do đó
$\mathop {\lim }\limits_{x \to - 2} \frac{{2x + 1}}{{{{\left( {x + 2} \right)}^2}}} = - \infty $
|