|
|
1.Phép tịnh tiến hệ toạ độ và công thức chuyển hệ toạ độ
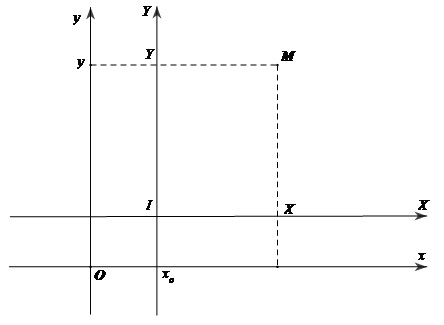
Giả sử $I$ là 1 điểm của mặt phẳng và $({x_0};{y_0})$ là tọa độ của điểm $I$ đối với hệ tọa độ $Oxy$, Gọi $IXY$ là hệ tọa độ mới có gốc là điểm $I$ và 2 trục $IX, IY$ theo thứ tự có cùng vecto đơn vị $\overrightarrow i ,\overrightarrow j $ với 2 trục $Ox, Oy$
Giả sử $M$ là một điểm bất kỳ của mặt phẳng. Gọi $(x; y)$ là tọa độ của điểm $M$ đối với hệ tọa độ $Oxy$ và $(X; Y)$ là tọa độ của điểm $M$ đối với hệ tọa độ $IXY$. Khi đó:
$\overrightarrow {OM} = \overrightarrow {OI} + \overrightarrow {IM} $
Hay
$\begin{gathered}
x\overrightarrow i + y\overrightarrow j = ({x_0}\overrightarrow i + {y_0}\overrightarrow j ) + (X\overrightarrow i + Y\overrightarrow j ) \\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = (X + {x_0})\overrightarrow i + (Y + {y_0})\overrightarrow j \\
\\
\end{gathered} $
Do đó
$\left\{ \begin{gathered}
x = X + {x_0} \\
y = Y + {y_0} \\
\end{gathered} \right.$
Các hệ thức trên gọi là công thức chuyển hệ tọa độ trong phép tịnh tiến theo vectơ $\overrightarrow {OI} $
2 .Phương trình của đường cong đối với hệ toạ độ mới
Giả sử $(\Im )$ là đồ thị của hàm số $y= f(x)$ đối với hệ tọa độ $Oxy$ đã cho. Khi đó phương trình của đường cong $(\Im )$ đối với hệ tọa độ $Oxy$ là $y = f(x)$
Phương trình của đường cong $(\Im )$ đối với hệ tọa độ $IXY$ là:
$Y = f(x + {x_0}) - {y_0}$
VÍ DỤ
Cho đường cong $(C)$ có phương trình là $Y = \frac{1}{2}{(x - 2)^3} - 1$ và điểm $I(2; - 1)$
a) Viết công thức luân chuyển hệ toạ độ trong phép tịnh tiến theo vectơ $\overrightarrow {OI} $
và viết phương trình của đường cong $(C)$ đối với hệ toạ độ $IXY$
a) Từ đó suy ra rằng $I$ là tâm đối xứng cuả đường cong $(C)$
Giải
a) Công thức luân chuyển hệ toạ độ trong phép tịnh tiến theo vectơ $\overrightarrow {OI} $ là
$\left\{ \begin{gathered}
x = X + 2 \\
y = Y - 1 \\
\end{gathered} \right.$
Phương trình của đương cong $(C)$ đối với hệ toạ độ $IXY$ là
$Y - 1 = \frac{1}{2}{X^3} - 1\,\,hay\,\,Y = \frac{1}{2}{X^3}$
b) Vì $\,Y = \frac{1}{2}{X^3}$ là một hàm số lẻ nên đồ thị $(C)$ của nó nhận gốc toạ độ $I$ là tâm đối xứng
|