|
|
Trong định lý 1 bài 3, ta đã biết: Nếu $y = f\left( x \right)$là một hàm liên tục và lấy giá trị không âm trên đoạn $\left[ {a;b} \right]$thì diện tích S của hình thang cong giới hạn bởi đồ thị hàm số $y = f\left( x \right)$, trục hoành và hai đường thẳng x = a, x = b là:
$S = \int\limits_a^b {f\left( x \right)dx} $
- Một cách tổng quát, ta có
Nếu hàm số $y = f\left( x \right)$ liên tục trên đoạn $\left[ {a;b} \right]$thì diện tích S của hình phẳng giới hạn bởi đồ thị hàm số $y = f\left( x \right)$, trục hoành và hai đường thẳng x = a, x = b là:
$S = \int\limits_a^b {\left| {f\left( x \right)} \right|dx} $ (1)
Ví dụ
Tính diện tích S của hình phẳng giới hạn bởi đồ thị hàm số $y = {x^3} - 1$ , đường thẳng $x = 2$, trục tung và trục hoành
Giải
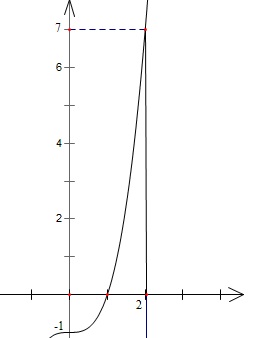
Đặt $f\left( x \right) = {x^3} - 1$
Ta thấy $f\left( x \right) \leqslant 0$ trên $\left[ {0;1} \right]$ và $f\left( x \right) \geqslant 0$ trên $\left[ {1;2} \right]$
Theo công thức (1), diện tích S của hình đang xét là
$\begin{gathered}
S = \int\limits_0^2 {\left| {{x^3} - 1} \right|dx} \\
\,\,\,\, = \int\limits_0^1 {\left( {1 - {x^3}} \right)dx} + \int\limits_1^2 {\left| {{x^3} - 1} \right|dx} \\
\,\,\,\, = \frac{3}{4} + \frac{{11}}{4} = \frac{7}{{12}} \\
\end{gathered} $
- Để tính diện tích S của hình phẳng giới hạn bởi đồ thị các hàm số $y = f\left( x \right)$, $y = g\left( x \right)$ liên tục trên đoạn $\left[ {a;b} \right]$ và hai đường thẳng $x = a, x = b$ ,ta có công thức sau:
$S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} $
- Để tính diện tích một số hình phẳng phức tạp hơn ta phải chia hình đã cho thành một số hình đợn giản mà ta đã biết cách tính diện tích.
CHÚ Ý
Tương tự (bằng cách coi x là hàm của biến y ), diện tích S của hình phẳng giới hạn bởi các đường cong $x = g\left( y \right)$, $x = h\left( y \right)$(g và h là hai hàm liên tục trên đoạn $\left[ {c;d} \right]$ và hai đường thẳng $y = c,\,\,\,y = d$ là
$S = \int\limits_c^d {\left| {g\left( y \right) - h\left( y \right)} \right|dy} $ (3)
|