|
|
1. Tính thể tích vật thể
Cho một vật thể trong không gian tọa độ Oxyz. Gọi B là phần của vật thể giới hạn bởi hai mặt phẳng vuông góc với trục Ox tại các điểm a và b.
Gọi S(x) là diện tích thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x(a⩽x⩽b)
Giả sử S=S(x) là một hàm số liên tục. Người ta chứng minh được rằng thể tích V của B là
V=b∫aS(x)dx (1)
Ví dụ: Cho khối chóp cụt có chiều cao h, diện tích đáy nhỏ và đáy lớn thứ tự là S0,S1. Khi đó thể tích V của nó là
V=h3(S0+√S0S1+S1)
Nhận xét: Khối chóp được coi là khối chóp cụt có S0=0. Vì vậy, thể tích V của khối chóp có chiều cao h và diện tích đáy S là
V=Sh3
2. Thể tích khối tròn xoay
-Một hình phẳng quay quanh 1 trục nào đó tạo nên 1 khối tròn xoay
- Cho hàm số y=f(x) liên tục, không âm trên [a;b]. Hình phẳng giới hạn bởi đồ thị hàm số y=f(x), trục hoành và hai đường thẳng x=a,x=b quay quanh trục hoành tạo nên một khối tròn xoay. Thể tích V của nó được tính theo công thức
V=πb∫af2(x)dx (2)
Ví dụ 2:
(Thể tích khối chỏm cầu). Cho một khối chỏm cầu bán kính R và chiều cao h. Chứng mịnh rằng thể tích V của khối chỏm cầu là
V=πh2(R−h3)
Giải
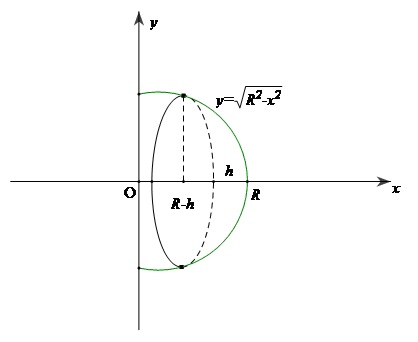
Trong mặt Oxy, xét hình phẳng giới hạn bởi cung tròn tâm O bán kính R có phương trình y=√R2−x2 , trục hoành và đường thẳng x=R−h(0<h⩽R). Quay hình phẳng đó quanh trục hoành ta thì được khối chỏm cầu bán kính R chiều cao h (hình 3.13 trang170)
Theo công thức (2) thể tích khối chỏm cầu là
V=πR∫R−h(R2−x2)dx=π(R2x−x33)|RR−h=π(R3−R33−R2(R−h)+(R−h)33)=πh2(R−h3)
Nhận xét: Khối bán cầu R được coi là khối chỏm cầu bán kính R và chiều cao h = R. Vì vậy, thể tích của khối bán cầu bán kính R là
V=πh2(R−h3)=2πR33
Do đó, thể tích hình cầu bán kính R là:
V=4πR33
- Tương tự, cho đường cong có phương trình x=g(y), trong đó g là hàm số liên tục và không âm trên đoạn [c;d]. Hình phẳng giới hạn bởi đường cong x=g(y), trục tung và hai đường thẳng y=c,y=d, quay quanh trục tung tạo nên một khối tròn xoay .Thể tích V của nó được tính theo công thức
V=πd∫cg2(y)dy (3)
Thật vậy, từ công thức (2) bằng cách xem x là hàm của biến y ta suy ra công thức (3)
-Thể tích khối nón cụt: Cho khối nón cụt có chiều cao h, bán kính đáy lớn và đáy nhỏ lần lượt là R và r. Thể tích khối nón cụt đó là:
V=13πh(R2+Rr+r2)
|