|
|
1.Phương trình tổng quát của đường thẳng
ĐỊNH NGHĨA:
- Vecto pháp tuyến của đường thẳng: Vectơ khác $\overrightarrow 0 $ , có giá vuông góc với đường thẳng $\Delta $ gọi là vectơ pháp tuyến của đường thẳng $\Delta $
- Trong mặt phẳng toạ độ , mọi đường thẳng đều có phương trình tổng quát dạng
${\text{ax}} + by + c = 0$, với ${{\text{a}}^2} + {b^2} \ne 0$
Ngược lại, ta có thể chứng minh được rằng: Mỗi phương trình dạng
${\text{ax}} + by + c = 0$, với ${{\text{a}}^2} + {b^2} \ne 0$
Đều là phương trình tổng quát của một đường thẳng xác định, nhận $\overrightarrow n = (a;\,\,b)$ là vectơ pháp tuyến
Ví dụ : Cho tam giác có ba đỉnh A=(-1 ;-1) , B=(-1;3) , C=(2;-4) viết phương trình tổng quát của đường cao kẻ từ A
GIẢI :
Đường cao cần tìm là đường thẳng đi qua A và nhận $\overrightarrow {BC} $ là một vectơ pháp tuyến. ta có $\overrightarrow {BC} = (3; - 7)$ và A=(-1 ;-1) nên theo (1) , phương trình tổng quát của đường cao đó là 3(x +1) – 7(y + 1)=0 hay 3x – 7y – 4 = 0.
CÁC DẠNG ĐẶC BIỆT CỦA PHƯƠNG TRÌNH TỔNG QUÁT
GHI NHỚ 1
Đường thẳng $by + c = 0$ song song hoặc trùng với trục $Ox$ (hình 67a trang77)
Đường thẳng $ax + c = 0$ song song hoặc trùng với trục $Oy$ (hình67b trang77)
Đường thẳng $ax + by = 0$ đi qua gốc toạ độ (hình 67c trang 77)
GHI NHỚ 2:
Đường thẳng có phương trình $\frac{x}{a} + \frac{y}{b} = 1\,\,\,\,\,(a \ne 0,b \ne 0)$ (2)
đi qua hai điểm $A(a;0)\& B(0;b)$ phương trình (2) được gọi là phương trình đường thẳng theo đoạn chắn
CHÚ Ý:
Xét đường thẳng $\Delta $ có phương trình tổng quát $ax + by + c = 0$
Nếu $b \ne 0$ thì phương trình trên đưa được về dạng
$y = kx + m$ (3)
với $k = - \frac{a}{b},\,\,m = - \frac{c}{b}$. Khi đó k là hệ số góc của đường thẳng và (3) gọi là phương trình của $\Delta $ theo hệ số góc.
Ý nghĩa hình học của hệ số góc
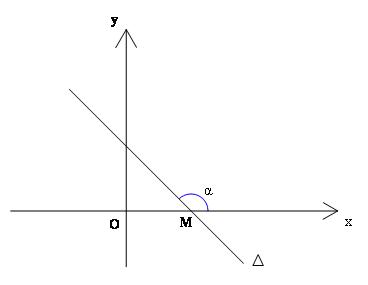
Xét đường thẳng $\Delta :y = kx + m$
Với$k \ne 0$, gọi M là giao điểm của $\Delta $ với trục Ox và Mt là tia của $\Delta $ nằm phía trên Ox. Khi đó, nếu $\alpha $ là góc hợp bởi hai tia Mt và Mx thì hệ số góc của đường thẳng $\Delta $ bằng tang của góc $\alpha $, tức là $k = \tan \alpha $.
Khi k = 0 thì $\Delta $ là đường thẳng song song hoặc trùng với Ox
2. VỊ TRI TƯƠNG ĐỐI CỦA HAI ĐƯỜNG THẲNG
Trong mặt phẳng toạ đô , cho hai đường thẳng${\Delta _1},\,\,{\Delta _2}$ có phương trình
$\begin{gathered}
{\Delta _1}:\,\,{a_1}x + {b_1}y + {c_1} = 0 \\
{\Delta _2}:\,\,{a_2}x + {b_2}y + {c_2} = 0 \\
\end{gathered} $
Vì số điểm chung của hai đường thẳng bằng số nghiệm của hệ gồm hai phương trình trên, nên từ kết quả của đại số ta có
a, Hai đường thẳng ${\Delta _1},\,\,{\Delta _2}$cắt nhau khi và chỉ khi
$\left| \begin{gathered}
{a_1}\,\,\,\,\,{b_1} \\
{a_2}\,\,\,\,\,{b_2}\, \\
\end{gathered} \right| \ne 0$;
b, Hai đường thẳng ${\Delta _1},\,\,{\Delta _2}$song song khi và chỉ khi
$\left| \begin{gathered}
{a_1}\,\,\,\,\,{b_1} \\
{a_2}\,\,\,\,\,{b_2}\, \\
\end{gathered} \right| = 0\,\,\,$và $\left| \begin{gathered}
{b_1}\,\,\,\,\,{c_1} \\
{b_2}\,\,\,\,\,{c_2}\, \\
\end{gathered} \right| = 0\,\,\,$
Hoặc $\left| \begin{gathered}
{a_1}\,\,\,\,\,{b_1} \\
{a_2}\,\,\,\,\,{b_2}\, \\
\end{gathered} \right| = 0\,\,\,$và $\left| \begin{gathered}
{c_1}\,\,\,\,\,{a_1} \\
{c_2}\,\,\,\,\,{a_2}\, \\
\end{gathered} \right| = 0\,\,\,$
b, Hai đường thẳng ${\Delta _1},\,\,{\Delta _2}$trùng nhau khi và chỉ khi
$\left| \begin{gathered}
{a_1}\,\,\,\,\,{b_1} \\
{a_2}\,\,\,\,\,{b_2}\, \\
\end{gathered} \right| = \left| \begin{gathered}
{b_1}\,\,\,\,\,{c_1} \\
{b_2}\,\,\,\,\,{c_2}\, \\
\end{gathered} \right| = \left| \begin{gathered}
{c_1}\,\,\,\,\,{a_1} \\
{c_2}\,\,\,\,\,{a_2}\, \\
\end{gathered} \right| = 0\,\,\,$
Trong trường hợp${a_2},\,\,{b_2},\,\,{c_2}$ đều khác 0 , ta có
${\Delta _1},\,\,{\Delta _2}$ cắt nhau $ \Leftrightarrow \frac{{{a_1}}}{{{a_2}}} \ne \frac{{{b_1}}}{{{b_2}}};$
${\Delta _1}//\,{\Delta _2} \Leftrightarrow \frac{{{a_1}}}{{{a_2}}} = \frac{{{b_1}}}{{{b_2}}} \ne \frac{{{c_1}}}{{{c_2}}}$
${\Delta _1} \equiv \,{\Delta _2} \Leftrightarrow \frac{{{a_1}}}{{{a_2}}} = \frac{{{b_1}}}{{{b_2}}} = \frac{{{c_1}}}{{{c_2}}}$
|