|
|
1. Định nghĩa phép đối xứng trục
Ta nhắc lại: Điểm $M’$ gọi là đối xứng với điểm $M$ qua đường thẳng $a$ nếu $a$ là đường trung trực của đoạn thẳng $MM’$. Nếu $M$ nằm trên a thì ta xem $M$ đối xứng với chính nó qua $a$
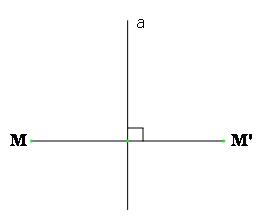
ĐỊNH NGHĨA
Phép đối xứng qua đường thẳng $a$ là phép biến hình biến mỗi điểm $M$ thành điểm $M’$ đối xứng với $M$ qua $a$.
2. Định lý
Phép đối xứng trục là một phép dời hình
Chú ý:
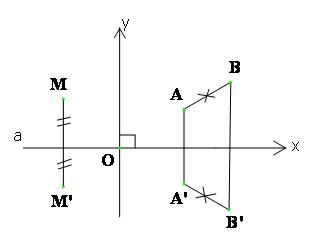
Qua hoạt động trên, ta thấy nếu phép đối xứng qua trục Ox biến điểm $M(x ; y )$ thành điểm $M'(x’ ; y’)$ thì
$\begin{cases}x^'=x \\ y^'= -y\end{cases}$
Công thức trên gọi là biểu thức tọa độ của phép đối xứng qua trục Ox
3. Trục đối xứng của một hình
Chúng ta hãy quan sát bốn hình sau đây (mỗi chữ cái là một hình)

Người ta nói hình thứ nhất và hình thứ hai có tính “cân xứng” vì với mỗi hình, có thể tìm thấy một đường thẳng sao cho phép đối xứng qua đường thẳng đó biến hình ấy thành chính nó. Các đường thẳng đó gọi là trục đối xứng của mỗi hình. Hai hình còn lại không “cân xứng” vì chúng không có những đường thẳng như vây.
ĐỊNH NGHĨA 2
Đường thẳng $d$ gọi là trục đối xứng của hình $(H)$ nếu phép đối xứng trục $Đ_{d} $ biến hình $(H)$ thành chính nó, tức là $Đ_{d}(H)=(H) $
Một hình có thể không có trục đối xứng, cũng có thể có một hay nhiều trục đối xứng.
|