|
|
1. Định nghĩa phép quay
ĐỊNH NGHĨA
Trong mặt phẳng cho một điểm $O$ cố định và góc lượng giác $\varphi $ không đổi. Phép biến hình biến điểm $O$ thành điểm $O$, biến mỗi điểm $M$ khác $O$ thành điểm $M’$ sao cho $OM = OM’$ và $\left( {OM,OM'} \right) = \varphi $ được gọi là phép quay tâm $O$ góc quay $\varphi $
2. Định lý
Phép quay là một phép dời hình
Chứng minh
Giả sử phép quay ${Q_{(O,\varphi )}}$ biến điểm M thành M’ và biến điểm N thành N’, trong đó O, M, N không thẳng hàng. Theo định nghĩa của phép quay, ta có $OM$=$OM'$;$ON$=$ON'$ và $\left( {OM,OM'} \right) = \left( {ON,ON'} \right) = \varphi $
Theo hệ thức Sa-lơ về góc lượng giác, ta có
$\left( {OM,ON} \right) = \left( {OM,OM'} \right) + \left( {OM',ON} \right) = \,\left( {ON,ON'} \right) + \left( {OM',ON} \right) = \left( {OM',ON'} \right)$
Suy ra = . Như vậy hai tam giác $MON$ và $M'ON'$ bằng nhau, do đó $M'N' = MN$. Trường hợp $O,M,N$ thẳng hàng, ta thấy ngay $M'N' = MN$.
3. Phép đối xứng tâm
ĐỊNH NGHĨA
Phép đối xứng tâm qua điểm $O$ là một phép biến hình mỗi điểm $M$ thành điểm $M’$ đối xứng với $M$ qua $O$, có nghĩa là $\overrightarrow {OM} + \overrightarrow {OM} ' = \overrightarrow 0 $
Kí hiệu và thuật ngữ: Phép đối xứng qua điểm $O$ thường được kí hiệu là ${Đ_O}$. Phép đối xứng qua 1 điểm còn gọi đơn giản là phép đối xứng tâm
Điểm $O$ được gọi là tâm đối xứng
Biểu thức tọa độ của phép đối xứng tâm:
Trong hệ tọa độ $Oxy$ cho điểm $I\left( {a;b} \right)$. Nếu phép đối xứng tâm ${Đ_I}$ biến điểm $M(x ; y )$ thành điểm $M'(x’ ; y’)$ thì $\left\{ \begin{gathered}
x' = 2a - x \\
y' = 2b - y \\
\end{gathered} \right.$
Công thức trên gọi là biểu thức tọa độ của phép đối xứng tâm $I$
Tâm đối xứng của một hình
Điểm O gọi là tâm đối xứng của một hình $(H)$ nếu phép đối xứng tâm ${Đ_0}$ biến hình $(H)$ thành chính nó, tức là ${Đ_0}(H) = (H)$.
4. Ứng dụng của phép quay
Bài toán 1
Cho hai tam giác đều $OAB$ và $OA’B’$ như hình vẽ. Gọi $C$ và $D$ lần lượt là trung điểm của các đoạn thẳng $AA’$ và $BB’$. Chứng minh rằng $OCD$ là tam giác đều.
Giải:
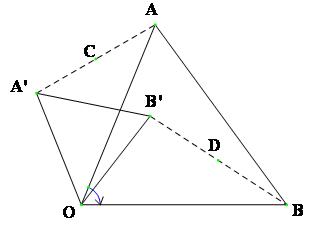
Xét phép quay $Q$ tâm O với góc quay bằng một góc lượng giác $\left( {OA,OB} \right)$. Rõ ràng $Q$ biến A thành B và biến A’ thành B’, nên $Q$ biến đoạn thẳng AA’ thành đoạn thẳng $BB’$. Từ đó suy ra $Q$ biến trung điểm C của AA’ thành trung điểm A của BB’. Do đó $OC = OD$ và . Vậy $OCD$ là tam giác đều.
|