|
|
1. Vị trí tương đối giữa hai đường thẳng phân biệt
ĐỊNH NGHĨA
Hai đường thẳng gọi là đồng phẳng nếu chúng cùng nằm trong một mặt phẳng.
Hai đường thẳng gọi là chéo nhau nếu chúng không đồng phẳng
Hai đường thẳng gọi là song song nếu chúng đồng phẳng không có điểm chung
2. Hai đường thẳng song song
Tính chất 1
Trong không gian qua một điểm nằm ngoài một đường thẳng có một và chỉ một đường thẳng song song với đường thẳng đó
Tính chất 2
Hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì song song với nhau.
ĐỊNH LÝ
Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến ấy hoặc đồng quy hoặc đôi một song song.
HỆ QUẢ
Nếu hai mặt phẳng cắt nhau lần lượt đi qua hai đường thẳng song song thì giao tuyến của chúng song song với hai đường thẳng đo (hoặc trùng với một trong hai đường thẳng đó)
Ví dụ
Cho hình chóp $S.ABCD$ có đáy là hình bình hành
a, Tìm giao tuyến của hai mặt phẳng $\left( {SAB} \right)$và $\left( {SCD} \right)$
b, Xác định thiết diện của hình chóp $S.ABCD$khi cắt bới mặt phẳng$\left( {MBC} \right)$trong đó M là một điểm nằm giữa hai điểm S và A.
Giải:
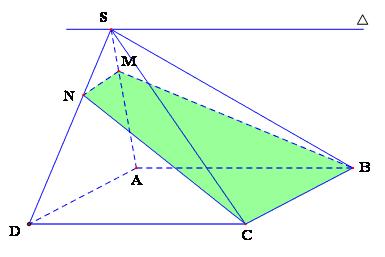
a, $mp\left( {SAB} \right)$ và $mp\left( {SCD} \right)$có điểm chung S và lần lượt đi qua hai đường thẳng song song AB và CD nên chúng cắt nhau theo giao tuyến $\vartriangle $đi qua S và song song với AB và CD.
b, $mp\left( {MBC} \right)$ và $mp\left( {SAD} \right)$lần lượt đi qua hai đường thẳng song song BC và AD và có điểm chung M nên giao tuyến của chúng là đường thẳng MN song song với $AD\left( {N \in SD} \right)$. Vậy thiết diện của hình chóp $S.ABCD$ khi cắt bởi$mp\left( {MBC} \right)$ là hình thanh MNCB.
|