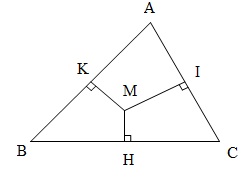Với mọi tam giác $ABC$ và điểm $M$ trong tam giác ta có
$\left\{ \begin{array}{l}
{S_a}\overrightarrow {MA}  + {S_b}\overrightarrow {Mb}  + {S_c}\overrightarrow {MC}  = \overrightarrow 0 \,\,\,\,\,\,\,\,\,\, &  &  & (1)\\
\frac{a}{{MH}}\overrightarrow {MH}  + \frac{b}{{MI}}\overrightarrow {MI}  + \frac{c}{{MK}}\overrightarrow {MK}  = \overrightarrow 0  &  &  & (2)
\end{array} \right.$

Biến đổi tương đương:
$M$ là trọng tâm $\Delta ABC$
\(\begin{array}{l}
\Leftrightarrow \overrightarrow {MA}  + \overrightarrow {MB}  + \overrightarrow {MC}  = \overrightarrow 0 \\
 \Leftrightarrow {S_a} = {S_b} = {S_c}\\
 \Leftrightarrow a.MH = b.MI = c.MK\\
 \Leftrightarrow \frac{{{a^2}}}{({\frac{a}{{MH}}})} = \frac{{{b^2}}}{({\frac{b}{{MI}}})} = \frac{{{c^2}}}{({\frac{c}{{MK}}})}
\end{array}\)
   \( \Leftrightarrow {a^2}\overrightarrow {MH}  + {b^2}\overrightarrow {MI}  + {c^2}\overrightarrow {MK}  = \overrightarrow 0 \)( theo $(2)$).

bạn có thể tham khảo bài  này nhé !
http://toan.hoctainha.vn/Thu-Vien/Bai-Tap/102598/bai-102598

Số có $6$ chữ số được tạo thành là $6! = 720$
Số có chứa $16$ là $5! = 120$
Số có chứa $61$ là $5! = 120$
Ở đây ta coi $16$ và $61$ là như nhau.
Vậy, số số tạo thành mà $1, 6$ không đứng cạnh nhau là: $720 – 240 = 480$ số.

Cách 1:
Gọi số cần lập là: $
\overline{abcdefgh}
$
* TH1: $
a=1
$
- Chọn 2 trong 7 vị trí còn lại cho số 1. Có $
C^{2}_{7}
$ cách chọn (vì hai số 1 giống nhau nên không liên quan tới thứ tự)
- Còn 5 vị trí ta xếp 5 số thuộc tập ${0,2,3,4,5} $xếp vào 5 vị trí còn lại. Có $
P_{5}
$ cách xếp.
TH1 có$
C^{2}_{7}.P_{5}=2520
$ (cách xếp)
* TH2:$
a\neq 1.
$
- Có 4 cách chọn a
- Chọn 3 vị trí trong 7 vị trí còn lại để xếp số 1. Có $
C^{3}_{7}
$ cách chọn.
- 4 vị trí còn lại ta sắp xếp các số còn lại. Có $
P_{4}
$cách xếp.
Vậy TH2 có $
4.C^{3}_{7}.P_{4}=3360
$ (cách)
Vậy có: $
3360+2520=5880
$ (số)