đây là đề thi tuyển sinh đại học khối B năm 2013

Câu a
Kí hiệu $X$ là tập hợp tất cả các số tự nhiên gồm $5$ chữ số khác nhau đôi một được lập thành từ $6$ chữ số $1, 3, 4, 5, 7, 8$

Xét \(x = \overline {{a_1}{a_2}{a_3}{a_4}{a_5}}  \in X\)

Nếu chọn \({a_5} = 1\) thì \(\overline {{a_1}{a_2}{a_3}{a_4}} \) ứng với một chỉnh hợp chập $4$ của $5$ phần tử $3, 4, 5, 7, 8$.

Vậy có \(A_5^4\) phần tử \(x \in X\) với chữ số hàng đơn vị bằng $1$. Tương tự ta có \(A_5^4\) phần tử \(x \in X\) với \({a_5} = 3\);… Vậy tổng số của tất cả các chữ số  hàng đơn vị của các phần tử \(x \in X\) là:
\(\left( {1 + 3 + 4 + 5 + 7 + 8} \right).A_5^4 = 28.120 = 3360\). Lập luận tương tự, tổng các chữ số hàng chục của các phần tử của $x$ là: $3360.10$,…

Vậy tổng của tất cả các phần tử của $x$ là:
$3360 + 3360.10 + 3360.100 + 3360.1000 + 3360.10000 = 3360.11111 = 37332960$

* Số các số có 6 chữ số khác nhau là:
 * Số các số có 6 chữ số khác nhau và đều khác $0$ là:
 * Số các số có 6 chữ số khác nhau và đều khác $1$ là:
 * Số các số có 6 chữ số khác nhau và không có cả $0$ và $1$ là:
                                                              $8.7.6.5.4.3=20160$ 
Vậy số các số có 6 chữ số khác nhau trong đó đều có mặt chữ số $0$ và $1$ là:

Em có thể xem và tham khảo nhé :
http://toan.hoctainha.vn/Thu-Vien/Ly-Thuyet/106312/phuong-trinh-tong-quat-cua-duong-thang

http://toan.hoctainha.vn/Thu-Vien/Chuyen-De/113570/viet-phuong-trinh-duong-thang-trong-khong-gian

http://toan.hoctainha.vn/Thu-Vien/Ly-Thuyet/113404/phuong-trinh-tong-quat-cua-duong-thang

Em có thể xem và tham khảo nhé :
http://toan.hoctainha.vn/Thu-Vien/Ly-Thuyet/106312/phuong-trinh-tong-quat-cua-duong-thang

http://toan.hoctainha.vn/Thu-Vien/Chuyen-De/113570/viet-phuong-trinh-duong-thang-trong-khong-gian

Lời giải này có yêu cầu trả vỏ sò để xem. Bạn hãy link trên để vào xem chi tiết

Lời giải này có yêu cầu trả vỏ sò để xem. Bạn hãy link trên để vào xem chi tiết

Lời giải này có yêu cầu trả vỏ sò để xem. Bạn hãy link trên để vào xem chi tiết

$I=\int\limits_{-1}^{0} \frac{dx}{x^{2} + 2x + 2} = $$\int\limits_{-1}^{0} \frac{dx}{(x+1)^2 +1}$
Đặt $x+1=\tan t \rightarrow dx = \frac{1}{\cos^2 t}dt = (\tan^2 t+1)dt$
Đổi cận: $ x: -1\rightarrow 0$
                $ t: 0\rightarrow \frac{\pi }{4}$

$\rightarrow I=\int\limits_{0}^{\frac{\pi }{4}} \frac{(\tan^2 t+1)dt}{\tan^2 t+1}= \int\limits_{0}^{\frac{\pi }{4}} dt=\frac{\pi }{4}$

Giả sử $A(a;0;0); B(0;b;0); C(0;0;c)$.

Do $OA,OB,OC$ đôi một vuông góc với nhau và $H$ là trực tâm của tam giác $ABC$ suy ra $OH\bot(ABC)$, nên $\overrightarrow{OH}=(2;1;1)$ là một vectơ pháp tuyến của $ABC: \frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1$
từ đó ta có $\frac{1}{a}:\frac{1}{b}:\frac{1}{c}=2:1:1$
Hay $b=c=2a$. Như vậy $(P)$ có dạng:
$ \frac{x}{a}+\frac{y}{2a}+\frac{z}{2a}=1   (1)$
Do $(P)$ qua $H(2;1;1)$ nên ta có phương trình:
$ \frac{2}{a}+\frac{1}{2a}+\frac{1}{2a}=1\Rightarrow a=3$.
Vậy phương trình $(P)$ có dạng: $ \frac{x}{3}+\frac{y}{6}+\frac{z}{6}=1$.

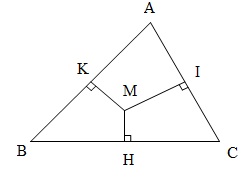Với mọi tam giác $ABC$ và điểm $M$ trong tam giác ta có
$\left\{ \begin{array}{l}
{S_a}\overrightarrow {MA}  + {S_b}\overrightarrow {Mb}  + {S_c}\overrightarrow {MC}  = \overrightarrow 0 \,\,\,\,\,\,\,\,\,\, &  &  & (1)\\
\frac{a}{{MH}}\overrightarrow {MH}  + \frac{b}{{MI}}\overrightarrow {MI}  + \frac{c}{{MK}}\overrightarrow {MK}  = \overrightarrow 0  &  &  & (2)
\end{array} \right.$

Biến đổi tương đương:
$M$ là trọng tâm $\Delta ABC$
\(\begin{array}{l}
\Leftrightarrow \overrightarrow {MA}  + \overrightarrow {MB}  + \overrightarrow {MC}  = \overrightarrow 0 \\
 \Leftrightarrow {S_a} = {S_b} = {S_c}\\
 \Leftrightarrow a.MH = b.MI = c.MK\\
 \Leftrightarrow \frac{{{a^2}}}{({\frac{a}{{MH}}})} = \frac{{{b^2}}}{({\frac{b}{{MI}}})} = \frac{{{c^2}}}{({\frac{c}{{MK}}})}
\end{array}\)
   \( \Leftrightarrow {a^2}\overrightarrow {MH}  + {b^2}\overrightarrow {MI}  + {c^2}\overrightarrow {MK}  = \overrightarrow 0 \)( theo $(2)$).

bạn có thể tham khảo bài  này nhé !
http://toan.hoctainha.vn/Thu-Vien/Bai-Tap/102598/bai-102598

Số có $6$ chữ số được tạo thành là $6! = 720$
Số có chứa $16$ là $5! = 120$
Số có chứa $61$ là $5! = 120$
Ở đây ta coi $16$ và $61$ là như nhau.
Vậy, số số tạo thành mà $1, 6$ không đứng cạnh nhau là: $720 – 240 = 480$ số.

Cách 1:
Gọi số cần lập là: $
\overline{abcdefgh}
$
* TH1: $
a=1
$
- Chọn 2 trong 7 vị trí còn lại cho số 1. Có $
C^{2}_{7}
$ cách chọn (vì hai số 1 giống nhau nên không liên quan tới thứ tự)
- Còn 5 vị trí ta xếp 5 số thuộc tập ${0,2,3,4,5} $xếp vào 5 vị trí còn lại. Có $
P_{5}
$ cách xếp.
TH1 có$
C^{2}_{7}.P_{5}=2520
$ (cách xếp)
* TH2:$
a\neq 1.
$
- Có 4 cách chọn a
- Chọn 3 vị trí trong 7 vị trí còn lại để xếp số 1. Có $
C^{3}_{7}
$ cách chọn.
- 4 vị trí còn lại ta sắp xếp các số còn lại. Có $
P_{4}
$cách xếp.
Vậy TH2 có $
4.C^{3}_{7}.P_{4}=3360
$ (cách)
Vậy có: $
3360+2520=5880
$ (số)

Ta có \(y = \frac{{3{{\left( {1 - {{\sin }^2}x} \right)}^2} + 4{{\sin }^2}x}}{{3{{\sin }^4}x + 2\left( {1 - {{\sin }^2}x} \right)}}\)
Đặt \(t = {\sin ^2}x;0 \le t \le 1\). Khi đó \(y = \frac{{3{t^2} - 2t + 3}}{{3{t^2} - 2t + 2}} = 1 + \frac{1}{{3{t^2} - 2t + 2}}\)
Xét hàm số
    \(f\left( t \right) = 3{t^2} - 2t + 2   (0 \le t \le 1)\)
\(\Rightarrow f'\left( t \right) = 6t - 2 = 0 \Leftrightarrow t = \frac{1}{3}\)
Ta có bảng biến thiên như hình vẽ: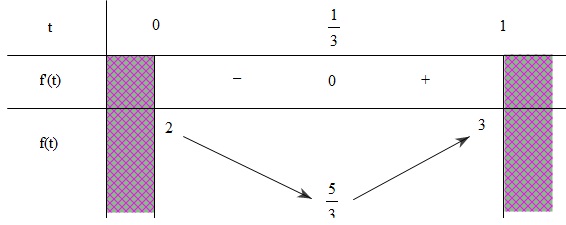


Suy ra \(\frac{5}{3} \le f\left( t \right) \le 3 \Leftrightarrow \frac{8}{5} \ge y \ge \frac{4}{3}\)
Vậy \(\min y  = \frac{4}{3}\)khi \({\sin ^2}x = 1\), chẳng hạn khi \(x = \frac{\pi }{2}\)
\(\max y  = \frac{8}{5}\)khi \({\sin ^2}x = \frac{1}{3}\)