|
|
giải đáp
|
một bạn hỏi trên faceboook
|
|
|
|
$(1+2x+3x^{2})^{10}$= $((1+2x)+(3x^{2}))^{10}$
Khai triển có số hạng tổng quát là:
$C^{k}_{10}$ . $(1+2x)^{k}$. $(3x^{2})^{10-k}$= $C^{k}_{10}$ . $C^{n}_{k}$. $1^{k-n}$. $(2x)^{n}$. $(3x^{2})^{10-k}$= $C^{k}_{10}$ . $C^{n}_{k}$. $1^{k-n}$. $2^{n}$. $3^{10-k}$. $x^{20+n-2k}$
Với n, k thỏa mãn các điều kiện sau: k$\leqslant $10, n$\leqslant $k, 20+n-2k=3
=> (k,n)= $\left\{ {(9,1), (10,3)} \right\}$
Vậy hệ số của $x^{3}$ trong khai triển đa thức là: 540+960= 1500
|
|
|
|
giải đáp
|
một bạn hỏi trên facebook
|
|
|
|
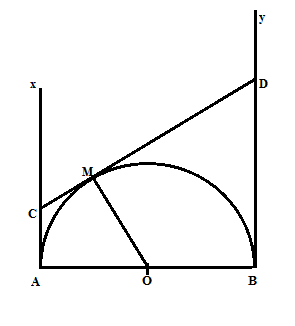
a/ Xét $\Delta$COA và $\Delta$COM có:
CO chung
$\widehat{CAO}$ = $\widehat{CMO}$= $90^{0}$
CA=CM=R
=> $\Delta$COA = $\Delta$COM (c.g.c)
=> CM=CA
Tương tự: $\Delta$DMO = $\Delta$DBO => DM=
DB
=> CM+DM= CA+DB= CD (đpcm)
b/ Theo chứng minh các tam giác bằng nhau
trên, ta có: $\widehat{COA}$ = $\widehat{COM}$, $\widehat{DOM}$ =
$\widehat{DOB}$
=> $\widehat{COM}$ +
$\widehat{DOM}$ = $\widehat{COA}$ +$\widehat{DOB}$= 1/2. $180^{0}$=
$90^{0}$ |
|
|
|
giải đáp
|
giúp mình
|
|
|
|
Gỉa sử đường tròn có tâm là I(x,y)
$\overrightarrow{AI}$(x-3,y-4) => $AI^{2}$ = $(x-3)^{2}+(y-4)^{2}$
$\overrightarrow{BI}$(x-4,y-1) => $BI^{2}$ = $(x-4)^{2}+(y-1)^{2}$
$\overrightarrow{CI}$(x-2,y+3) => $CI^{2}$ = $(x-2)^{2}+(y+3)^{2}$
$\overrightarrow{DI}$(x+1,y-6) => $DI^{2}$ = $(x+1)^{2}+(y-6)^{2}$
Ta giải hệ 3 phương trình sau:
$AI^{2}=BI^{2}$ => x-3y+4=0
$AI^{2}=CI^{2}$ => x+7y-6=0
$AI^{2}=DI^{2}$ => -2x+y-3=0
=> x=-1, y=1
Vậy A,B,C,D nội tiếp trong đường tròn tâm I(-1,1) (đpcm)
|
|
|
|
giải đáp
|
bài toán xác suất nè
|
|
|
|
Bài này bạn đã hỏi một lần rồi mà :)
http://toan.hoctainha.vn/Hoi-Dap/Cau-Hoi/114423/ai-lam-dc-bai-vui-nay
|
|
|
|
giải đáp
|
Bài toán về hình chóp.
|
|
|
|
 a/ mp(OMN) $\cap $ (SAD)= MN, có MN//AD, mà AD $\in $(ABCD) => Giao tuyến (d) của mp(OMN) với (ABCD) là đường thẳng song song với AD, mà AD// BC => (d)// BC (đpcm) b/ (d) cắt AB tại Q, CD tại P. Có PQ qua tâm O và //BC và AD => PQ là đường trung bình của hình bình hành=> P là trung điểm của CD, Q là trung điểm của AB => MQ // SB, NP//SC (đpcm) |
|
|
|
giải đáp
|
Trục tọa độ
|
|
|
|
Lời giải này có yêu cầu trả vỏ sò để xem. Bạn hãy link trên để vào xem chi tiết
|
|
|
|
giải đáp
|
hình chóp
|
|
|
|
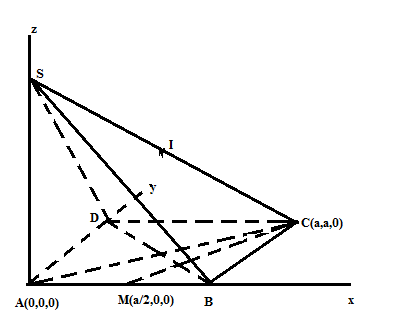 Gắn hình vẽ vào hệ trục tọa độ trong không gian sao cho A trùng gốc O, AB trùng Ox, AD trùng Oy, AS trùng Oz Khị đó, tọa độ các điểm là: A(0,0,0), M(a/2,0,0), C(a,a,0), I(a/2,a/2,a/2) Ta có : $\overrightarrow{CM}$= (-a/2,-a,0)= (1,2,0) => Phương trình CM: x+2y-3a=0 => d(I, CM)= $\frac{3a}{2\sqrt{5}}$ |
|
|
|
|
|
giải đáp
|
Không cần tính hãy so sánh
|
|
|
|
1995. 1995= (1990+5). (1990+5)= $1990^{2}$+ 10.1990+ 25
1991. 1999= (1990+1).(1990+9)= $1990^{2}$+ 10.1990+ 9
Vậy 1995. 1995 > 1991. 1999
|
|
|
|
đặt câu hỏi
|
Giaỉ tích số!
|
|
|
|
CMR: quá trình lặp $x_{n}$ = cos$(x_{n-1})$ hội tụ $\forall x_{0}\in (-\infty ,+\infty )$
|
|
|
|
giải đáp
|
em hỏi bài này
|
|
|
|
+/ Tìm x sao cho MN có GTNN?
Ta có: MC vuông góc với DC và CC' => MC vuông góc svới (DCC'D') => MC vuông góc với CN
=> $\Delta$MCN vuông tại C => $MN^{2}= MC^{2}+CN^{2}$
Có: MC= a-x; $CN^{2}=DC^{2}+DN^{2}= a^{2}+x^{2}$
=> $MN^{2}$= 2$a^{2}$-2a.x+ 2$x^{2}$= 2. $(a-1/2.x)^{2}$+ 3/2.$x^{2}$
MN nhỏ nhất <=> $MN^{2}$ nhỏ nhất <=> a= 1/2.x
Vậy khi x= 2a thì MN nhận GTNN
|
|
|
|
giải đáp
|
giải hộ mình câu hình học toạ độ không gian lớp 12 mình đang cần gấp
|
|
|
|
b/ AC= 2.OA= 4; BD= 2.OB= 2 Giao tuyến của (SDC) và mp(AMN) là MN sao cho MN// DC (N thuộc SD)
$V_{SABCD}$= 1/3. SO. $S_{ABCD}$= 1/3.SO. 1/2. AC.BD= $\frac{4\sqrt{2}}{3}$
Ta có: $\frac{V_{SABMN}}{V_{SABCD}}$= $\frac{V_{SABM}}{V_{SABC}}$+ $\frac{V_{SAMN}}{V_{SACD}}$= 1/2+1/2. 1/2= 3/4
=> $V_{SABMN}$= $\sqrt{2}$ |
|
|
|
giải đáp
|
giải hộ mình câu hình học toạ độ không gian lớp 12 mình đang cần gấp
|
|
|
|
a/ SA qua A(2,0,0), $\overrightarrow{SA}$= (2,0,-$\sqrt{2}$) BM qua B(0,1,0), $\overrightarrow{BM}$= (-1,-1,$\sqrt{2}$) Khoảng cách giữa SA và BM là: h= $\frac{\left| {\left[ {\overrightarrow{SA},\overrightarrow{BM}} \right].\overrightarrow{AB}} \right|}{\left[ {\overrightarrow{SA},\overrightarrow{BM}} \right]}$ = $\frac{\sqrt{2}}{8}$ |
|
|
|
giải đáp
|
giúp mình bài hình
|
|
|
|
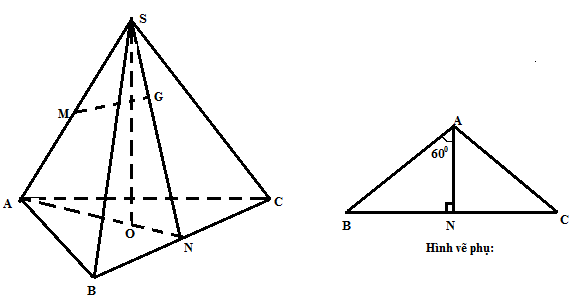 Gọi N là trung diểm của BC, gọi O là trọng tâm $\Delta$ABC. Từ O dựng OS vuông góc với mp (ABC) Trong mp (SAN) kẻ MG vuông góc với SN (1) Ta có: BC vuông góc với AN BC vuông góc với SO => BC vuông góc với (SAN) => BC vuông góc với MG (2) (1)(2) => MG vuông góc với mp(SBC) => MG= d(M, (SBC)) Có: $\Delta$SNB vuông tại N=> $SN^{2}$ = $(2\sqrt{2})^{2}- a^{2}$ Có: $\Delta$ ANB vuông tại N => tan A= $\frac{BN}{AN}$ => AN= a/$\sqrt{3}$ Áp dụng hệ thức lượng với $\Delta$SAN: cosASN= $\frac{AS^{2}+SN^{2}-AN^{2}}{2.AS.SN}$= $\frac{4-\frac{a^{2}}{3}}{\sqrt{2}.\sqrt{8-a^{2}}}$ = cosMSG = $\frac{SG}{SM}$ => SG= $\frac{4-\frac{a^{2}}{3}}{\sqrt{2}.\sqrt{8-a^{2}}}$. $\sqrt{2}$= $\frac{4-\frac{a^{2}}{3}}{\sqrt{8-a^{2}}}$ Ta có: SGM là $\Delta$ vuô ngtại G => $MG^{2}$ = $SM^{2}-SG^{2}$= $\frac{a^{2}/9+ \frac{2a^{2}}{3}}{8- a^{2}}$ => MG= $\sqrt{\frac{a^{2}/9+ \frac{2a^{2}}{3}}{8- a^{2}}}$ |
|
|
|
giải đáp
|
ai làm dc bài vui này
|
|
|
|
b/ Các bộ phận B,C,D có diện tích bằng nhau, A có diện tích gấp đôi B và máy bay bị trúng viên đạn
Xác suất để 1 viên đạn trúng vào một bộ phận A,B,C,D lần lượt là: 0,4; 0,2; 0,2; 0,2
+) TH1: 2 viên đạn trúng vào cùng một bộ phận
P(A)+p(B)+P(C)+P(D)= 2.P(A)+3.P(B)= $0,4^{2}$ + 3. $0,2^{2}$= 0,28
+) TH2: 2 viên đạn trúng vào 2 bộ phận liền kề nhau
P(AB)+P(BA)+P(BC)+P(CB)+P(CD)+P(DC)
= 2. P(AB)+ 4. P(BC)
= 2.0,4.0,2+ 4.0,2.0,2= 0,32
Vậy xác suất để máy bay rơi là: 0,28+0,32= 0,6
|
|