|
|
|
|
giải đáp
|
Nhị thức Newton(3).
|
|
|
|
Số hạng tổng quát khi khai triển là: $C^{k}_{4}$. $(2x- x^{2})^{k}$= $C^{k}_{4}$. $C^{t}_{k}$. $(2x)^{k-t}$. $(-x^{2})^{t}$= $(-1)^{t}$. $C^{k}_{4}$. $C^{t}_{k}$. $2^{k-t}$. $x^{k+t}$ với k$\leq $4, t$\leq $k
Khai triển chứa $x^{7}$ => k+t=7 và thỏa mãn 2 điều kiện trên
=> k=4, t=3
=> Hệ số của số hạng chứa $x^{7}$ trong khai triển là: (-1). $C^{4}_{4}$. $C^{3}_{4}$. $2^{1}$= -8
|
|
|
|
giải đáp
|
Nhị thức Newton(1).
|
|
|
|
Số hạng tổng quát của khai triển là: $C^{k}_{8}$. $x^{2k}$. $C^{t}_{k}$. $1^{k-t}$. $(-x)^{t}$= $(-1)^{t}$. $C^{k}_{8}$. $C^{t}_{k}$. $x^{2k+t}$ với t$\leq $k
$x^{8}$ trong khai triển => 2k+t= 8
=> (k,t)= $\left\{ {(3,2), (4,0)} \right\}$
=> Hệ số số hạng khai triển $x^{8}$ là: $C^{3}_{8}$+ $C^{4}_{8}$
|
|
|
|
giải đáp
|
ngày này k đi chơi, lên hỏi mọi người mấy bài vậy
|
|
|
|
c/ $S_{OMN}$=16 => OM.ON=32 => a.b=32 => b=32/a
=> M(a,0), N(0, 32/a) => $\overrightarrow{MN}$( -a, 32/a) => MN= $\sqrt{a^{2}+(32/a)^{2}}$
MN: 32/a. (x-2)+ a. (y-4)=0
Khi đó: d(O, MN)= $\frac{\frac{-64}{a}-4a}{\sqrt{(32/a)^{2}+a^{2}}}$
=> $S_{OMN}$= 1/2. d(O, MN). MN= $\frac{-32}{a}$ - 2a = 16
=> a=-4, b=-8
=> $\overrightarrow{MN}$=(4,-8)= (1,-2)
=> MN:2x+y+8=0
|
|
|
|
giải đáp
|
ngày này k đi chơi, lên hỏi mọi người mấy bài vậy
|
|
|
|
M$\in $Ox => M(a,0)
N$\in $Oy => N(0,b)
a/ A(2,4) là trung điểm => $\begin{cases}\frac{a+0}{2}=2 \\ \frac{0+b}{2}=4 \end{cases}$
=> a=4, b=8
=> $\overrightarrow{MN}$=( -4,8)= (-1,2)
=> MN: 2x+y-8=0
|
|
|
|
giải đáp
|
Bài toán về thiết diện của hình chóp.
|
|
|
|
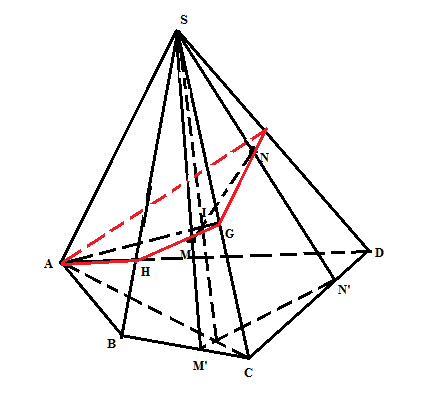 Gọi M' =SM$\cap $BC, N'= SN$\cap $CD Trong mp( ABCD), gọi O= M'N'$\cap $AC Trong mp( SM'N') gọi I= MN$\cap $SO Trong mp( SAC) gọi G= AI$\cap $SC Trong mp( SCD) gọi T= GN$\cap $SD Trong mp( SBC) gọi H= GM$\cap $SB Vậy thiết diện của mp(SMN) với hình chóp là (AHGT). |
|
|
|
bình luận
|
Hình không gian
:)) Nâu cóa gì, mà iem lười suy nghĩ quá đấy, bài này viết ra hơi dài thôi chứ dễ nhìn hình mà
|
|
|
|
|
|
|
|
sửa đổi
|
bài tập về nhà.mọi người jup nhé, em cần gấp
|
|
|
|
$\overrightarrow{AB}$=(3,-4) => AB=5$\overrightarrow{AC}$=(1,0) =>AC=1=>AC<ABPhương trình đường AC: -y+4=0Trên AC lấy C' => C' có tọa độ (x,4) sao cho AC'=5$\overrightarrow{AC'}$=( x+a,0)=> $\left| {x+1} \right|$=5 => x=4 hoặc x=-6Trường hợp x=-6 loại vì khi đó $\overrightarrow{AC'}$ ngược chiều với $\overrightarrow{AC}$Khi AD là phân giác trong thì D sẽ là trung điểm của BC'=> D(3,2)=> $\overrightarrow{AD}$(4,-2)= (2,-1)=> AD: x+2y-7=0b/ Gọi D' là chân đường phân giác trong của AD=> D' = BC$\cap $ADMà $\overrightarrow{BC}$=(2,-4)=(1,-2)=> BC: 2x+y-4=0=> D'(1/3,10/3)
a/ $\overrightarrow{AB}$=(3,-4) => AB=5$\overrightarrow{AC}$=(1,0) =>AC=1=>AC<ABPhương trình đường AC: -y+4=0Trên AC lấy C' => C' có tọa độ (x,4) sao cho AC'=5$\overrightarrow{AC'}$=( x+a,0)=> $\left| {x+1} \right|$=5 => x=4 hoặc x=-6Trường hợp x=-6 loại vì khi đó $\overrightarrow{AC'}$ ngược chiều với $\overrightarrow{AC}$Khi AD là phân giác trong thì D sẽ là trung điểm của BC'=> D(3,2)=> $\overrightarrow{AD}$(4,-2)= (2,-1)=> AD: x+2y-7=0b/ Gọi D' là chân đường phân giác trong của AD=> D' = BC$\cap $ADMà $\overrightarrow{BC}$=(2,-4)=(1,-2)=> BC: 2x+y-4=0=> D'(1/3,10/3)
|
|
|
|
giải đáp
|
bài tập về nhà.mọi người jup nhé, em cần gấp
|
|
|
|
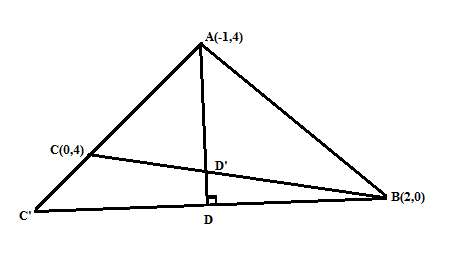 a/ $\overrightarrow{AB}$=(3,-4) => AB=5 $\overrightarrow{AC}$=(1,0) =>AC=1 =>AC<AB Phương trình đường AC: -y+4=0 Trên AC lấy C' => C' có tọa độ (x,4) sao cho AC'=5 $\overrightarrow{AC'}$=( x+a,0) => $\left| {x+1} \right|$=5 => x=4 hoặc x=-6 Trường hợp x=-6 loại vì khi đó $\overrightarrow{AC'}$ ngược chiều với $\overrightarrow{AC}$ Khi AD là phân giác trong thì D sẽ là trung điểm của BC'=> D(3,2) => $\overrightarrow{AD}$(4,-2)= (2,-1) => AD: x+2y-7=0 b/ Gọi D' là chân đường phân giác trong của AD=> D' = BC$\cap $AD Mà $\overrightarrow{BC}$=(2,-4)=(1,-2) => BC: 2x+y-4=0 => D'(1/3,10/3) |
|
|
|
sửa đổi
|
Hình không gian
|
|
|
|
a/ Gọi G là trung điểm của AB.=> Góc giữa (SAB) và (ABCD) là $\widehat{SGO}$= $60^{0}$Xét $\Delta$SOG vuông tại O có: SO= GO. tan$60^{0}$= a$\sqrt{3}$=> $V_{S.ABCD}$= 1/3. SO. $S_{ABCD}$= $\frac{4\sqrt{3}a^{3}}{3}$Trong mp(SAC) gọi H= SO$\cap $CITrong mp(SBD) qua H kẻ MN //BD. Khi đó mp(CMIN) chính là mp qua CI và // BDTa có: $\frac{V_{S.IMCN}}{V_{S.ABCD}}$= $\frac{V_{S.IMC}}{V_{S.ABC}}$+ $\frac{V_{S.INC}}{V_{S.ACD}}$ = $\frac{SI}{SA}$. $\frac{SM}{SB}$ +$\frac{SI}{SA}$. $\frac{SN}{SD}$= 2. $\frac{SI}{SA}$. $\frac{SN}{SD}$ (1)Có H là trọng tâm $\Delta$SAC => SH/SO= SN/SD= 2/3Thay vào (1) => $\frac{V_{S.IMCN}}{V_{S.ABCD}}$= 2/3=> $V_{S.IMCN}$= $\frac{8\sqrt{3}a^{3}}{9}$ b/ Trong mp (SAC) kẻ SK vuông góc với IC (2) Có BD//MN, BD vuông góc với (SAC) => MN vuông góc với (SAC)=> MN vuông góc với SK (3) (2), (3) => SK= d(S, (CMIN)) Có CH= $\sqrt{OH^{2}+OC^{2}}$= a$\sqrt{\frac{7}{3}}$ Mà H là trọng tâm $\Delta$ SAC => CI= 3/2. CH= $\frac{a\sqrt{21}}{2}$ Có MN= 2/3 BD= $\frac{a. 4\sqrt{2}}{3}$ => $S_{CMIN}$= 1/2. CI.MN= $\frac{a^{2}.\sqrt{42}}{3}$ Mà $V_{S.CMIN}$= 1/3. SK. $S_{CMIN}$ => SK= $\frac{8a}{\sqrt{14}}$
a/ Gọi G là trung điểm của AB.=> Góc giữa (SAB) và (ABCD) là $\widehat{SGO}$= $60^{0}$Xét $\Delta$SOG vuông tại O có: SO= GO. tan$60^{0}$= a$\sqrt{3}$=> $V_{S.ABCD}$= 1/3. SO. $S_{ABCD}$= $\frac{4\sqrt{3}a^{3}}{3}$Trong mp(SAC) gọi H= SO$\cap $CITrong mp(SBD) qua H kẻ MN //BD. Khi đó mp(CMIN) chính là mp qua CI và // BDTa có: $\frac{V_{S.IMCN}}{V_{S.ABCD}}$= $\frac{V_{S.IMC}}{V_{S.ABC}}$+ $\frac{V_{S.INC}}{V_{S.ACD}}$ = $\frac{SI}{SA}$. $\frac{SM}{SB}$ +$\frac{SI}{SA}$. $\frac{SN}{SD}$= 2. $\frac{SI}{SA}$. $\frac{SN}{SD}$ (1)Có H là trọng tâm $\Delta$SAC => SH/SO= SN/SD= 2/3Thay vào (1) => $\frac{V_{S.IMCN}}{V_{S.ABCD}}$= 2/3=> $V_{S.IMCN}$= $\frac{8\sqrt{3}a^{3}}{9}$ b/ Trong mp (SAC) kẻ SK vuông góc với IC (2) Có BD//MN, BD vuông góc với (SAC) => MN vuông góc với (SAC)=> MN vuông góc với SK (3) (2), (3) => SK= d(S, (CMIN)) Có CH= $\sqrt{OH^{2}+OC^{2}}$= a$\sqrt{\frac{7}{3}}$ Mà H là trọng tâm $\Delta$ SAC => CI= 3/2. CH= $\frac{a\sqrt{21}}{2}$ Có MN= 2/3 BD= $\frac{a. 4\sqrt{2}}{3}$ => $S_{CMIN}$= 1/2. CI.MN= $\frac{a^{2}.\sqrt{42}}{3}$ Mà $V_{S.CMIN}$= 1/3. SK. $S_{CMIN}$ => SK= $\frac{8a}{\sqrt{14}}$
|
|
|
|
giải đáp
|
Hình không gian
|
|
|
|
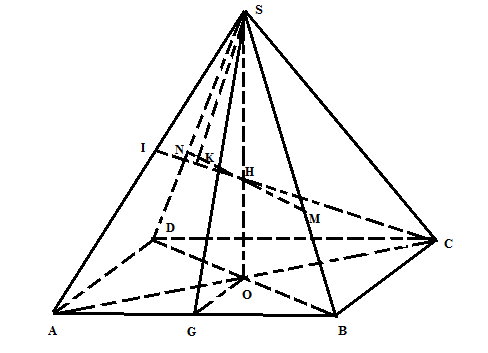 a/ Gọi G là trung điểm của AB. => Góc giữa (SAB) và (ABCD) là $\widehat{SGO}$= $60^{0}$ Xét $\Delta$SOG vuông tại O có: SO= GO. tan$60^{0}$= a$\sqrt{3}$ => $V_{S.ABCD}$= 1/3. SO. $S_{ABCD}$= $\frac{4\sqrt{3}a^{3}}{3}$ Trong mp(SAC) gọi H= SO$\cap $CI Trong mp(SBD) qua H kẻ MN //BD. Khi đó mp(CMIN) chính là mp qua CI và // BD Ta có: $\frac{V_{S.IMCN}}{V_{S.ABCD}}$= $\frac{V_{S.IMC}}{V_{S.ABC}}$+ $\frac{V_{S.INC}}{V_{S.ACD}}$ = $\frac{SI}{SA}$. $\frac{SM}{SB}$ +$\frac{SI}{SA}$. $\frac{SN}{SD}$= 2. $\frac{SI}{SA}$. $\frac{SN}{SD}$ (1) Có H là trọng tâm $\Delta$SAC => SH/SO= SN/SD= 2/3 Thay vào (1) => $\frac{V_{S.IMCN}}{V_{S.ABCD}}$= 2/3 => $V_{S.IMCN}$= $\frac{8\sqrt{3}a^{3}}{9}$ b/ Trong mp (SAC) kẻ SK vuông góc với IC (2) Có BD//MN, BD vuông góc với (SAC) => MN vuông góc với (SAC)=> MN vuông góc với SK (3) (2), (3) => SK= d(S, (CMIN)) Có CH= $\sqrt{OH^{2}+OC^{2}}$= a$\sqrt{\frac{7}{3}}$ Mà H là trọng tâm $\Delta$ SAC => CI= 3/2. CH= $\frac{a\sqrt{21}}{2}$ Có MN= 2/3 BD= $\frac{a. 4\sqrt{2}}{3}$ => $S_{CMIN}$= 1/2. CI.MN= $\frac{a^{2}.\sqrt{42}}{3}$ Mà $V_{S.CMIN}$= 1/3. SK. $S_{CMIN}$ => SK= $\frac{8a}{\sqrt{14}}$ |
|
|
|
|
|
sửa đổi
|
khối chóp
|
|
|
|
Gọi G là trung điểm DCTrong mp(SHG) kẻ IN vuông góc với SG. (1)Ta có: DC vuông góc với HG, DC vuông góc với SH => DC vuông góc với mp(SHG) => DC vuông góc với IN (2) (1), (2) => IN vuông góc với (SDC). Theo giả thiết có IN=hXét $\Delta$SNI đồng dạng với $\Delta$SHG => $\frac{NI}{HG}$ =$\frac{SI}{SG}$Có SG= $\sqrt{SH^{2}+HG^{2}}$=$\sqrt{4SI^{2}+(a/2)^{2}}$=> $\frac{2h}{a}$= $\frac{SI}{\sqrt{4SI^{2}+(a/2)^{2}}}$=> SI= $\frac{ah}{\sqrt{a^{2}-4h^{2}}}$=> SH= $\frac{2ah}{\sqrt{a^{2}-4h^{2}}}$=> $V_{S.ABCD}$= 1/3. SH. $S_{ABCD}$= $\frac{2a^{3}h}{3\sqrt{a^{2}-4h^{2}}}$
Gọi G là trung điểm DCTrong mp(SHG) kẻ IN vuông góc với SG. (1)Ta có: DC vuông góc với HG, DC vuông góc với SH => DC vuông góc với mp(SHG) => DC vuông góc với IN (2) (1), (2) => IN vuông góc với (SDC). Theo giả thiết có IN=hXét $\Delta$SNI đồng dạng với $\Delta$SHG => $\frac{NI}{HG}$ =$\frac{SI}{SG}$Có SG= $\sqrt{SH^{2}+HG^{2}}$=$\sqrt{4SI^{2}+(a/2)^{2}}$=> $\frac{2h}{a}$= $\frac{SI}{\sqrt{4SI^{2}+(a/2)^{2}}}$=> SI= $\frac{ah}{\sqrt{a^{2}-4h^{2}}}$=> SH= $\frac{2ah}{\sqrt{a^{2}-4h^{2}}}$=> $V_{S.ABCD}$= 1/3. SH. $S_{ABCD}$= $\frac{2a^{3}h}{3\sqrt{a^{2}-4h^{2}}}$
|
|
|
|
giải đáp
|
khối chóp
|
|
|
|
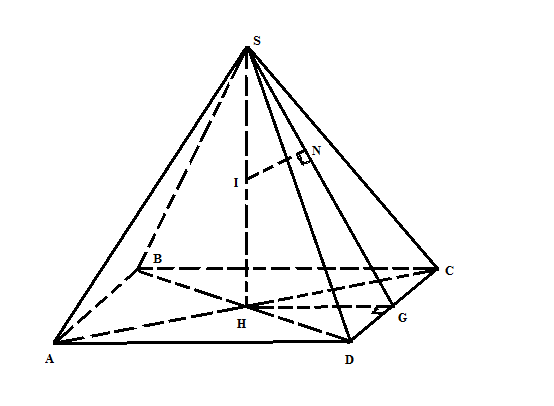 Gọi G là trung điểm DC Trong mp(SHG) kẻ IN vuông góc với SG. (1) Ta có: DC vuông góc với HG, DC vuông góc với SH => DC vuông góc với mp(SHG) => DC vuông góc với IN (2) (1), (2) => IN vuông góc với (SDC). Theo giả thiết có IN=h Xét $\Delta$SNI đồng dạng với $\Delta$SHG => $\frac{NI}{HG}$ =$\frac{SI}{SG}$ Có SG= $\sqrt{SH^{2}+HG^{2}}$=$\sqrt{4SI^{2}+(a/2)^{2}}$ => $\frac{2h}{a}$= $\frac{SI}{\sqrt{4SI^{2}+(a/2)^{2}}}$ => SI= $\frac{ah}{\sqrt{a^{2}-4h^{2}}}$ => SH= $\frac{2ah}{\sqrt{a^{2}-4h^{2}}}$ => $V_{S.ABCD}$= 1/3. SH. $S_{ABCD}$= $\frac{2a^{3}h}{3\sqrt{a^{2}-4h^{2}}}$ |
|
|
|
sửa đổi
|
giúp mình bài thể tích nhé
|
|
|
|
Trên AC lấy C' sao cho AC'= a, trên AD lấy D' sao cho AD'= aKhi đó ta đi tính thể tích tứ diện đều ABC'D' (do các mặt đều là tam giác đều)Gọi G là trung điểm C'D\Gọi O là trọng tâm $\Delta$BC'D', ta có AO vuông góc với mp (BC'D')Xét $\Delta$AOG có $AO^{2}$= $AG^{2}$-$OG^{2}= $$(a\sqrt{3}/2)^{2}$ - $(\frac{a\sqrt{3}}{6})^{2}$= 4$a^{2}$/9 => AO=2a/3Có $S_{BC'D'}$ =1/2. BG.C'D'= $\frac{a^{2}\sqrt{3}}{4}$=> $V_{A.BC'D'}$= $\frac{a^{3}\sqrt{3}}{18}$Tỉ lệ thể tích giữa 2 khối chóp tam giác: $\frac{V_{ABC'D'}}{V_{ABCD}}$= $\frac{AB}{AB}$. $\frac{AC'}{AC}$. $\frac{AD'}{AD}$= a/b. a/c= $\frac{a^{2}}{bc}$=> $V_{ABCD}$= $\frac{abc\sqrt{3}}{18}$
Trên AC lấy C' sao cho AC'= a, trên AD lấy D' sao cho AD'= aKhi đó ta đi tính thể tích tứ diện đều ABC'D' (do các mặt đều là tam giác đều)Gọi G là trung điểm C'DGọi O là trọng tâm $\Delta$BC'D', ta có AO vuông góc với mp (BC'D')Xét $\Delta$AOG có $AO^{2}$= $AG^{2}$-$OG^{2}= $$(a\sqrt{3}/2)^{2}$ - $(\frac{a\sqrt{3}}{6})^{2}$= 4$a^{2}$/9 => AO=2a/3Có $S_{BC'D'}$ =1/2. BG.C'D'= $\frac{a^{2}\sqrt{3}}{4}$=> $V_{A.BC'D'}$= $\frac{a^{3}\sqrt{3}}{18}$Tỉ lệ thể tích giữa 2 khối chóp tam giác: $\frac{V_{ABC'D'}}{V_{ABCD}}$= $\frac{AB}{AB}$. $\frac{AC'}{AC}$. $\frac{AD'}{AD}$= a/b. a/c= $\frac{a^{2}}{bc}$=> $V_{ABCD}$= $\frac{abc\sqrt{3}}{18}$
|
|