|
|
giải đáp
|
giup mik nha
|
|
|
|
Ta có : $\left. \begin{array}{l}
a({a^{logb}}) = logb.loga\\
log({b^{loga}}) = loga.logb
\end{array} \right\} \Rightarrow log({a^{logb}}) = log({b^{loga}}) \Leftrightarrow {a^{logb}} =
{b^{loga}}$
|
|
|
|
giải đáp
|
Tích phân cần giúp.
|
|
|
|
$I=\int_1^2 \dfrac{1}{x(x^{10}+1)^2}dx=\int_1^2 \dfrac{x^9}{x^{10}(x^{10}+1)^2}dx$
đặt $x^{10}+1 = t \Rightarrow 10x^9 dx = dt$ $I = \dfrac{1}{10}\int \dfrac{1}{(t-1).t^2}dt =\dfrac{1}{10} \int \bigg (-\dfrac{1}{t^2}-\dfrac{1}{t}+\dfrac{1}{t-1} \bigg )dt$
em tự làm nốt nhé !
|
|
|
|
giải đáp
|
Tích phân cần giúp.
|
|
|
|
Gợi ý $I=\int_1^2 \dfrac{\sqrt[3]{\dfrac{x^3 +x}{x^2}}}{x^3}dx=\int_1^2 \dfrac{\sqrt[3]{1+\dfrac{1}{x^2}}}{x^3}dx$
đặt $\sqrt[3]{1+\dfrac{1}{x^2}}=t \Rightarrow 1+\dfrac{1}{x^2} =t^3 \Rightarrow -\dfrac{2}{x^3}dx=3t^2 dt $
Vậy $I =-\dfrac{1}{2}\int 3t^3 dt=-\dfrac{3}{8}t^4 +C$ tự đổi cận và thế vào nhé |
|
|
|
giải đáp
|
$\sqrt{x^2-8x+15}$ $\leq$ $\sqrt{4x^2-18x+18}$ - $\sqrt{x^2+2x-15}$
|
|
|
|
$\sqrt{ x^{2} -8x +15}+ \sqrt{ x^{2} +2x-15} \leq \sqrt{ 4 x^{2} -18x +18}$
Điều
kiện : $\begin{cases} x^{2} -8x +15 \geq 0 \\ x^{2} +2x-15 \geq 0
\\ 4 x^{2} -18x +18 \geq 0 \end{cases} \Leftrightarrow
\begin{cases} x \leq 3, x \geq 5 \\ x \leq -5, x \geq 3 \\ x \leq
\frac{ 3}{2}, x \geq 3 \end{cases} \Leftrightarrow x \geq 5 $
Bất
phương trình : $\sqrt{\left( x-5 \right).\left( x-3\right) }+
\sqrt{\left( x+5 \right).\left( x-3 \right) } \leq \sqrt{\left(
x-3 \right) \left( 4x-6 \right) } $
$\Leftrightarrow \sqrt{ x-3} \left( \sqrt{ x-5}+ \sqrt{ x+5} \right) \leq \sqrt{ x-3}. \sqrt{ 4x-6}$
Với $x \geq 5 \Rightarrow \sqrt{ x-3}>0 :$ chia hai vế của bất phương trình cho $\sqrt{ x-3}$, ta được :
$\sqrt{ x-5}+ \sqrt{ x+5} \leq \sqrt{ 4x-6}$
$\Leftrightarrow x-5+x+5+2 \sqrt{ x^{2} -25} \leq \sqrt{ 4x-6}$
$\Leftrightarrow 2\sqrt{ x^{2} -25} \leq 2x-6$
$\Leftrightarrow x^{2} -25 \leq x^{2} -6x +9 \Leftrightarrow 6x \leq 39 \Leftrightarrow x \leq \frac{ 17}{3}$
Vậy $5 \leq x \leq \frac{ 17}{3}$
Với $x \leq -5$
Bất
phương trình: $\sqrt{ \left( 5-x \right) \left( 3-x \right)} +
\sqrt{ \left(-x-5 \right) \left( 3-x \right)} \leq \sqrt{ \left(
3-x \right) \left( 6-4x \right)} $
$\Leftrightarrow \sqrt{ 3-x}. \left( \sqrt{ 5-x}+ \sqrt{ -5-x} \right) \leq \sqrt{ 3-x} . \sqrt{ 6-4x}$
$\Leftrightarrow \sqrt{ 5-x}+ \sqrt{ -5-x} \leq \sqrt{ 6-4x}$ do $\sqrt{ 3-x} >0; x \leq -5$
$\Leftrightarrow 5-x-5-x+ 2 \sqrt{ x^{2} -25} \leq 6-4x$
$\Leftrightarrow \sqrt{ x^{2} -25} \leq 3- x$
$\Leftrightarrow x^{2} -25 \leq 9 – 6x + x^{2} \Leftrightarrow 6x \leq 34$
$\Leftrightarrow x \leq \frac{ 17}{3}$ Giao với $x \leq -5$ được $x \leq -5$
Vậy nghiệm của bất phương trình là : $\boxed {x \leq -5}$ hay $ \boxed {5 \leq x \leq \frac{ 17}{3}, x=3}$
|
|
|
|
giải đáp
|
phương pháp quy nạp
|
|
|
|
với $n=1$ VT$= \frac{1}{2}+\frac{1}{3}+\frac{1}{4}=\frac{13}{12}$
$=> (1)$ đúng với $n =1$
giả sử $(1)$ đúng với $n=k$ hay
$\frac{1}{k+1}+\frac{1}{k+2}+......+\frac{1}{3k+1} > 1$
cần chứng minh $(1)$ đúng với $n=k+1$
ta có $VT = \frac{1}{k+2}+\frac{1}{k+3}+....+\frac{1}{3k+1}+ \frac{1}{3k+2}+\frac{1}{3k+3}+\frac{1}{3k+4}$
$>1+\frac{1}{3k+2}+\frac{1}{3k+3}+\frac{1}{3k+4}> 1$ (với mọi $k\in N$)
suy ra đcmp
|
|
|
|
giải đáp
|
$\int\limits_{0}^{3ln2}\frac{dx}{(\sqrt[3]{e^x}+2)^2}$
|
|
|
|
Ta có $I = \int\limits_0^{3\ln 2} {\frac{{{e^{\frac{x}{3}}}dx}}{{{e^{\frac{x}{3}}}{{({e^{\frac{x}{3}}} + 2)}^2}}}} $
Đặt $u=e^{\frac{x}{3}}\Rightarrow $$3du = {e^{\frac{x}{3}}}dx$;
Đổi cận $x = 0 \Rightarrow u = 1;x = 3\ln 2 \Rightarrow u = 2$
Ta
được $I = \int\limits_1^2 {\frac{{3du}}{{u{{(u + 2)}^2}}}}
=3$$\int\limits_1^2 {\left( {\frac{1}{{4u}} - \frac{1}{{4(u + 2)}}}
\right.\left. { - \frac{1}{{2{{(u + 2)}^2}}}} \right)} du$
$=3\left.
{\left( {\frac{1}{4}\ln \left| u \right| - \frac{1}{4}\ln \left| {u + 2}
\right| + \frac{1}{{2(u + 2)}}} \right)} \right|_1^2$
$\boxed{= \frac{3}{4}\ln (\frac{3}{2}) - \frac{1}{8}} $
|
|
|
|
giải đáp
|
giải chi tiết giúp mình với
|
|
|
|
Đặt
$t = \pi - x \Rightarrow dt = - dx$
Đổi cận $\begin{cases} x=0 \rightarrow t=\pi \\ x=\pi \rightarrow t=0 \end{cases}$
$\begin{array}{l}
\Rightarrow I =- \int\limits_\pi^0 {\frac{{\left( {\pi - t}
\right)\sin t}}{{1 + c{\rm{o}}{{\rm{s}}^2}t}}} dt= \int\limits_0^\pi
{\frac{{\left( {\pi - t} \right)\sin t}}{{1 + c{\rm{o}}{{\rm{s}}^2}t}}}
dt = \pi \int\limits_0^\pi {\frac{{\sin t}}{{1 +
c{\rm{o}}{{\rm{s}}^2}t}}} dt - I\\
\Rightarrow 2I = \pi
\int\limits_0^\pi {\frac{{\sin t}}{{1 + c{\rm{o}}{{\rm{s}}^2}t}}} dt =
- \pi \int\limits_0^\pi {\frac{{d(\cos t)}}{{1 +
c{\rm{o}}{{\rm{s}}^2}t}}} = -\pi \arctan \cos t|_0^\pi=\pi \left(
{\frac{\pi }{4} +\frac{\pi }{4}} \right)\\
\Rightarrow \boxed{I =\frac{\pi^2}{4} }
\end{array}$
|
|
|
|
giải đáp
|
ứng dụng của tích phân
|
|
|
|
câu $1$
Vì $y = \frac{x}{{\sqrt {1 - {x^4}} }} > 0 \forall x \in \left( {0;\frac{1}{{\sqrt 2 }}} \right)$ nên diện tích cần tính là:
$S = \int\limits_0^{\frac{1}{{\sqrt 2 }}} {\frac{{xdx}}{{\sqrt {1 - {x^4}} }}} $
Đặt $t = {x^2} \Rightarrow S = \int\limits_0^{\frac{1}{2}} {\frac{{\frac{1}{2}dt}}{{\sqrt {1 -
{t^2}} }}} $
Đặt $\left\{ \begin{array}{l}
t = \sin u\\- \frac{\pi }{2} \le u \le \frac{\pi }{2}
\end{array} \right. \Rightarrow S = \frac{1}{2}\int\limits_0^{\frac{\pi }{6}} {\frac{{\cos
u}}{{\cos u}}du} =\frac{1}{2}u|^{\frac{\pi}{6}}_0= \frac{\pi }{{12}}$
ĐS : $S=\frac{\pi}{12}$ (đvdt)
|
|
|
|
giải đáp
|
Cấp số cộng
|
|
|
|
Theo giả thiết ta có :
$\begin{array}{l}
tan\frac{A}{2} + tan\frac{C}{2} = 2tan\frac{B}{2}\\
\Leftrightarrow
\frac{{\sin \frac{{A +
C}}{2}}}{{c{\rm{os}}\frac{A}{2}c{\rm{os}}\frac{C}{2}}} = 2\frac{{\sin
\frac{B}{2}}}{{c{\rm{os}}\frac{B}{2}}}\\
\Leftrightarrow 2{\cos ^2}\frac{B}{2} = 4\sin \frac{B}{2}c{\rm{os}}\frac{A}{2}c{\rm{os}}\frac{C}{2}\\
\Leftrightarrow 1 + \cos B = 2\sin \frac{B}{2}(c{\rm{os}}\frac{{A + C}}{2} + c{\rm{os}}\frac{{A - C}}{2})\\
\Leftrightarrow 1 + \cos B = 1 - \cos B + \cos A + \cos C\\
\Leftrightarrow 2\cos B = \cos A + \cos C\\
\Rightarrow dpcm
\end{array}$
Nhận xét :
Bài toán có ý nghĩa nếu ta chỉ ra rằng lớp các tam giác không đều $ABC$ thỏa mãn hệ thức
$tan\frac{A}{2} + tan\frac{C}{2} = 2tan\frac{B}{2}$ ($*$) là khác rỗng
Xét tam giác $ABC$có $A = {90^0} \Rightarrow tan\frac{A}{2} = 1,\cos A = 0$
Đặt $tan\frac{B}{2} = x \Rightarrow tg\frac{C}{2} = 2x - 1 \Rightarrow 2x - 1 > 0$ hay $\frac{1}{2} < x < 1$
Ta có $\cos B = \frac{{1 - {x^2}}}{{1 + {x^2}}};\cos C = \frac{{1 - {{(2x - 1)}^2}}}{{1 + {{(2x - 1)}^2}}}$
Ta có (*) $ \Leftrightarrow \cos A + \cos C = 2\cos B$
$\begin{array}{l}
\Leftrightarrow 2.\frac{{1 - {x^2}}}{{1 + {x^2}}} = \frac{{1 - {{(2x - 1)}^2}}}{{1 + {{(2x - 1)}^2}}}\\
\Leftrightarrow 2(1 - \frac{{2{x^2}}}{{1 + {x^2}}}) = 1 - \frac{{2{{(2x - 1)}^2}}}{{1 + {{(2x - 1)}^2}}}\\
\Leftrightarrow 1 = \frac{{4{x^2}}}{{1 - {x^2}}} - \frac{{2{{(2x - 1)}^2}}}{{1 + {{(2x - 1)}^2}}}\\
\Leftrightarrow
(1 - {x^2})\left[ {1 + {{(2x - 1)}^2}} \right] = 4{x^2}\left[ {1 +
{{(2x - 1)}^2}} \right] - 2(1 + {x^2}){(2x - 1)^2}\\
\Leftrightarrow 1 + {x^2} + (1 + {x^2}){(2x - 1)^2} = 4{x^2} + 4{x^2}{(2x - 1)^2} - 2(1 + {x^2}){(2x - 1)^2}\\
\Leftrightarrow 1 - 3{x^2} = {(2x - 1)^2}\left[ {4{x^2} - 3(1 + {x^2})} \right]\\
\Leftrightarrow {x^4} - {x^3} - 2{x^2} + 3x - 1 = 0\\
\Leftrightarrow (x - 1)({x^2} + x + 1) = 0(**)
\end{array}$
Vì $x > \frac{1}{2}$ nên từ $(**)$ suy ra :
$\begin{array}{l}
tan\frac{A}{2} + tan\frac{C}{2} = 2tan\frac{B}{2} \Leftrightarrow x = \frac{{\sqrt 5 - 1}}{2}\\
\Rightarrow \cos C = \frac{{1 - tan^2\frac{C}{2}}}{{1 + tan^2\frac{C}{2}}} = \frac{{\sqrt 5 }}{5}
\end{array}$
Như
vậy tồn tại tam giác $ABC$ không đều thỏa mãn hệ thức đã cho.Một trong
các tam giác đó là tam giác vuông $ABC$ tại $B$ với $C = \arccos
\frac{{\sqrt 5 }}{5}$
|
|
|
|
giải đáp
|
toán 10
|
|
|
|
Chọn hệ trục tọa độ $Oxy$ với $B\equiv O,A\in Oy,C\in Ox$ khi đó:
$A(0;h),B(0;0),C(b;0),D(a;h)$ với $a,b,h>0$
Ta có : $4=\overrightarrow {AB}.\overrightarrow {AC}=(0;-h)(b;-h)=h^2\Leftrightarrow h=2\Leftrightarrow AB=2 $
$9=\overrightarrow {CA}.\overrightarrow {CB}=(-b;h)(-b;0)=b^2\Leftrightarrow b=3\Leftrightarrow BC=3 $
$6=\overrightarrow {CB}.\overrightarrow {CD}=(-b;0)(a-b;h)=-3(a-3)\Leftrightarrow a=1\Leftrightarrow AD=1 $
$CD^2=(a-b)^2+h^2=4+4=8\Leftrightarrow CD=2\sqrt{2} $
|
|
|
|
|
|
giải đáp
|
hình oxyz kiểm tra 1 tiết
|
|
|
|
câu $1$
Gọi $\overrightarrow{m} $ là vtcp của $(d_1)$, khi đó $\overrightarrow{m}(m; 2; -3) $
(P) chứa $(d)\Rightarrow (P)$ thuộc chùm mặt phẳng xác định bởi $(d)$ có dạng:
$(P): A(x+2y-3z+1)+B(2x-3y+z+1)=0$
$\Leftrightarrow (A+2B)x+(2A-3B)y+(B-3A)z+A+B=0 (1)$
Khi đó $(P)$ có vtpt $\overrightarrow{n_1}(A+2B; 2A-3B; B-3A) $
1. Vì $(P)//(d_1) \Leftrightarrow \overrightarrow{n_1} $ vuông góc với $\overrightarrow{m} \Leftrightarrow m(A+2B)+2(2A-3B)-3(B-3A)=0 $
$\Leftrightarrow B=\frac{(13+m)A}{9-2m} $
Thay $B=\frac{(13+m)A}{9-2m} $ vào $(1)$ , ta được :
$(P): 35x-(11+7m)y+7(m-2)z+22-m=0$
|
|
|
|
giải đáp
|
hình oxyz 12
|
|
|
|
1. Ta có ngay:
$(S): \begin{cases}Tâm I(1; 2; 3) \\ bán kính R= \sqrt{14} \end{cases} $
2. Gọi $A; B; C$ theo thứ tự là giao điểm của (S) với $Ox; Oy Oz$ ta có ngay:
$A(2; 0; 0); B(0; 4; 0); C(0; 0; 6)$
Khi đó, phương trình mặt phẳng (ABC) được cho bởi:
$(ABC): \frac{x}{2}+ \frac{y}{4}+ \frac{z}{6}=1 \Leftrightarrow (ABC): 6x+3y+2z-12=0 $
|
|
|
|
giải đáp
|
HÌNH OXYZ 12
|
|
|
|
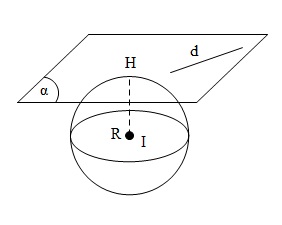 Vì mặt phẳng $(\alpha )$ chứa $d$ nên $(\alpha )$ thuộc chùm mặt phẳng có dạng $m(8x-11y+8z-30)+n(x-y-2z)=0(m^2+n^2\neq 0)$ $\Leftrightarrow (8m+n)x+(-11m-n)y+(8mm-2n)z-30m=0 (\alpha )$ Mặt cầu $(S)$ có tâm $I(-1;3;-2), R=\sqrt{1+9+4+15}=\sqrt{29} $ Vì $(\alpha )$ tiếp xúc với mặt cầu $(S)\Leftrightarrow d(I(\alpha ))=R$ $\Leftrightarrow \frac{|-8m-n-33m-3n-16m+4n-30m|}{\sqrt{(8m+n)^2+(-11m-n)^2+(8m-2n)^2} } =\sqrt{29} $ $\Leftrightarrow |-87|=\sqrt{29}.\sqrt{249m^2+6n^2+6mn} $ $\Leftrightarrow (87)^2=29(249m^2+6mn+6n^2)$ $\Leftrightarrow 261m^2=249m^2+6mn+6n^2$ $\Leftrightarrow 12m^2-6mn-6n^2=0\Leftrightarrow 2m^2-mn-n^2=0$ Chọn $\left\{ \begin{array}{l} n=1\\ 2m^2-m-1=0\Leftrightarrow m=1, m=-\frac{1}{2} \end{array} \right. $ $\Leftrightarrow
\left\{ \begin{array}{l} m=1\\ n=1 \end{array} \right. $ hoặc $\left\{
\begin{array}{l} m=-\frac{1}{2} \\ n=1 \end{array} \right. $ $m=1$ và $n=1:(\alpha ):9x-12y+6z-30=0\Leftrightarrow 3x-4y+2z-10=0 (\alpha_1 )$ $m=-\frac{1}{2} $ và $n=1:(\alpha ):-3x+\frac{9}{2}y-6z+15=0 $ $\Rightarrow -6x+9y-12z+30=0\Leftrightarrow 2x-3y+4z-10=0 (\alpha_2 )$ Vậy có hai phương trình mặt phẳng $(\alpha )$ thỏa mãn yêu cầu bài toán: $(\alpha_1 ):3x-4y+2z-10=0; (\alpha_2 ):2x-3y+4z-10=0$ |
|
|
|
giải đáp
|
HÌNH OXYZ 12
|
|
|
|
Mặt phẳng song song với $3x - 2y - 3z - 7 = 0$ có phương trình tổng quát dạng $3x - 2y - 3z + D = 0$.
Mặt phẳng này đi qua $A\left( {3,\, - 2,\, - 4} \right) \Leftrightarrow D = - 25$.
Do
đó mặt phẳng (P) chứa $A\left( {3,\, - 2,\, - 4} \right)$ và song với
$3x - 2y - 3z - 7 = 0$ có phương trình là $3x - 2y - 3z - 25 =
0\,\, \left( 2 \right)$
Đường thẳng
$(d)$:$\frac{{x - 2}}{3} = \frac{{y + 4}}{{ - 2}} = \frac{{z - 1}}{2}$
có phương trình tham số: $x = 3t + 2;\,y = - 2t - 4;\,z = 2t + 1$ thế
vào $(2)$ $t = 2$.
Do đó $(d)$ cắt $(P)$ tại $M\left( {8,\, - 8,\,\,5} \right)$
Đường
thẳng đi qua $A\left( {3, - 2, - 4} \right),\,M\left( {8, - 8,\,\,5}
\right)$ có phương trình $\frac{{x - 3}}{5} = \frac{{y + 2}}{{ - 6}} =
\frac{{z + 4}}{9}$ là đường thẳng qua A và song song với $3x - 2y - 3z -
7 = 0$ đồng thời cắt đường thẳng $\frac{{x - 2}}{3} = \frac{{y + 4}}{{ -
2}} = \frac{{z - 1}}{2}$
Vậy $\frac{{x - 3}}{5} = \frac{{y + 2}}{{ - 6}} = \frac{{z + 4}}{9}$ chính là đường thẳng cần tìm.
|
|