|
|
giải đáp
|
Toán 9
|
|
|
|
Lời giải này có yêu cầu trả vỏ sò để xem. Bạn hãy link trên để vào xem chi tiết
|
|
|
|
giải đáp
|
Toán 9
|
|
|
|
Lời giải này có yêu cầu trả vỏ sò để xem. Bạn hãy link trên để vào xem chi tiết
|
|
|
|
giải đáp
|
Cực trị.
|
|
|
|
Đặt
$\begin{cases}a=x+1 \\ b=y+1 \end{cases}\Rightarrow 0 \le x,y \le 1$.
Ta sẽ chứng minh $P \ge 1$ bằng cách chứng minh $a+b \ge a^2+b^2-ab$.
Thậy vậy
$\Leftrightarrow x+y+2 \ge (x+1)^2+(y+1)^2-(x+1)(y+1)$
$\Leftrightarrow 1+xy \ge x^2+y^2$
Mặt khác điều này hiển nhiên đúng do
$\begin{cases}x \ge x^2 \\ y\ge y^2\\(1-x)(1-y) \ge 0 \end{cases}\Leftrightarrow\begin{cases}x \ge x^2 \\ y\ge y^2\\1+xy \ge x+y \end{cases} \Rightarrow 1+xy \ge x^2+y^2$
Vậy $\min P =1 \Leftrightarrow (x,y)\in \{ (1,0),(0,1),(1,1)\}\Leftrightarrow (a,b)\in \{ (1,2),(2,1),(2,2)\}$
|
|
|
|
giải đáp
|
giải pt
|
|
|
|
Điều kiện $\begin{cases}x \ge -1 \\ x^{2}+x-3>0\end{cases}$ PT $\Leftrightarrow x^{2}+x-3=3\sqrt{x^{3}+1}$ $\Leftrightarrow (x^{2}+x-3)^2=9(x^{3}+1)$ $\Leftrightarrow x^4-7x^3-5x^2-6x=0$ $\Leftrightarrow x^3-7x^2-5x-6=0$ PT bậc ba này không có nghiệm đẹp. Để xem cách giải PT bậc ba tổng quát bạn có thể tham khảo phương pháp Cardano trên Google nhé. Pt có nghiệm duy nhất 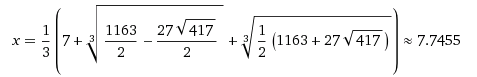 |
|
|
|
giải đáp
|
bài nữa rùi đi ăn cơm này.hehe
|
|
|
|
Giả sử rằng PT có nghiệm thì tất cả các biểu thức trong căn phải không âm.
Ta sẽ chứng minh điều sau
$$\sqrt{x+\sqrt{x^2-x+1} }<\sqrt{x+1+\sqrt{x^2+x+1} }+1$$
với mọi $x$ là cho các biểu thức có nghĩa.
Thật vậy,
+ Xét $x \ge 0$ thì hiển nhiên có
$0 < x^2-x+1 \le x^2+x+1$
$\Leftrightarrow x+\sqrt{x^2-x+1}<x+1+\sqrt{x^2+x+1}$
$\Leftrightarrow \sqrt{x+\sqrt{x^2-x+1} }<\sqrt{x+1+\sqrt{x^2+x+1} }+1$
+ Xét $x < 0$ thì
$0 < x^2-x+1 < x^2-2x+1=(1-x)^2$
$\Leftrightarrow \sqrt{x^2-x+1}<1-x$
$\Leftrightarrow x+\sqrt{x^2-x+1}<1$
$\Leftrightarrow \sqrt{x+\sqrt{x^2-x+1} }<\sqrt{x+1+\sqrt{x^2+x+1} }+1$
Tóm lại PT đã cho vô nghiệm.
|
|
|
|
giải đáp
|
bài tiếp nhé, mọi người cùng tham gia
|
|
|
|
Điều kiện $x > 2.$
PT
$\Leftrightarrow \sqrt[4]{\dfrac{x-1}{x-2}}+4m+(m+3) \sqrt[4]{\dfrac{x-2}{x-1}}=0$
Đặt $t= \sqrt[4]{\dfrac{x-1}{x-2}}>1$, thì PT
$\Leftrightarrow t+4m+(m+3)\dfrac{1}{t}=0\Leftrightarrow m(4+\dfrac{1}{t})=-\dfrac{3}{t}-t$
$\Leftrightarrow m=f(t)=\dfrac{-3-t^2}{4t+1}$
Lập bảng biến thiên của $f(t)$ trên $t>1$ ta suy ra $m <f(1)=-\dfrac{4}{5}$
|
|
|
|
giải đáp
|
giải nhé moij người
|
|
|
|
Điều kiện $x \ge 1.$
PT
$\Leftrightarrow m= \dfrac{-3\sqrt{x-1}+2\sqrt[4]{x^2-1}}{\sqrt{x+1}}=-3\sqrt{\dfrac{x-1}{x+1}}+2\sqrt[4]{\dfrac{x-1}{x+1}}$
Đặt $\begin{cases}t=\sqrt[4]{\dfrac{x-1}{x+1}}\Rightarrow 0 \le x <1 \\ m=f(t)=-3t^2+2t \end{cases}$
Lập bảng biến thiên của hàm $f(t)=-3t^2+2t$ trên $0 \le x <1$ ta có
$\underbrace{-1}_{\min_{[0,1)} f(t) } < f(t) \le \underbrace{\dfrac{1}{3}}_{\max_{[0,1)} f(t) }\Leftrightarrow \boxed{-1 < m \le\dfrac{1}{3} }$
|
|
|
|
giải đáp
|
toan 9
|
|
|
|
Bạn xem tại đây nhé
http://toan.hoctainha.vn/Hoi-Dap/Cau-Hoi/114779/tinh-tong
|
|
|
|
giải đáp
|
bài này!!!
|
|
|
|
Điều kiện $x \ge 0.$
Hiển nhiên có các bđt sau
$\begin{cases}x^2+1 \ge 2x\\ x^6+x^4 \ge 2x^5 \end{cases}\Rightarrow x^6+x^4+x^2+1 \ge 2(x^5+x)$
Đặt
$a=\sqrt{x^5+x^3+x}, b=\sqrt{x^2(x^2-x+1)}, c=\sqrt{(x^2+1)^3} $
Ta có
$(a+b)^2 \le 2(a^2+b^2) =2(x^5+x^4+x^2+x) \le x^6+x^4+x^2+1+2x^4+2x^2=(x^2+1)^3=c^2$
Như vậy với Điều kiện $x \ge 0$ ta luôn có
$(a+b)^2 \le c^2 \Leftrightarrow a+b \le c\Leftrightarrow a \le c-b$.
Vậy tập nghiệm của BPT là $x \ge 0.$
|
|
|
|
giải đáp
|
Giải bất phương trình
|
|
|
|
Điều kiện $x \ge 0.$
Hiển nhiên có các bđt sau
$\begin{cases}x^2+1 \ge 2x\\ x^6+x^4 \ge 2x^5 \end{cases}\Rightarrow x^6+x^4+x^2+1 \ge 2(x^5+x)$
Đặt
$a=\sqrt{x^5+x^3+x}, b=\sqrt{x^2(x^2-x+1)}, c=\sqrt{(x^2+1)^3} $
Ta có
$(a+b)^2 \le 2(a^2+b^2) =2(x^5+x^4+x^2+x) \le x^6+x^4+x^2+1+2x^4+2x^2=(x^2+1)^3=c^2$
Như vậy với Điều kiện $x \ge 0$ ta luôn có
$(a+b)^2 \le c^2 \Leftrightarrow a+b \le c\Leftrightarrow a \le c-b$.
Vậy tập nghiệm của BPT là $x \ge 0.$
|
|
|
|
giải đáp
|
Giải hệ phương trình
|
|
|
|
Từ PT thứ nhất ta có $x^3=y^3-7$.
Thay vào PT thứ hai ta có
$y^3-7-y^2+x=-2\Rightarrow x=5-y^3+y^2$.
Thay trở lại Pt thứ nhất ta có
$y^3-(5-y^3+y^2)^3-7=0$
$\Leftrightarrow (y-2)(y^8-y^7+y^6-14y^5+2y^4-11y^3+54y^2+33y+66)=0$
Kiểm tra rằng thấy PT $y^8-y^7+y^6-14y^5+2y^4-11y^3+54y^2+33y+66=0$ vô nghiệm nên hệ có nghiệm duy nhất
$x=1, y=2$.
|
|
|
|
giải đáp
|
giải bài này
|
|
|
|
Trừ theo từng vế của hai PT ta được
$-3x+2xy+8y+23=0\Leftrightarrow x=\dfrac{8y+23}{3-2y}$
Thay vào PT thứ nhất ta được
$\left ( \dfrac{8y+23}{3-2y} \right )^2+4y^2-4.\dfrac{8y+23}{3-2y}+12y+11=0$
$\Leftrightarrow y^4 +4y^2 +27y +22=0$
$\Leftrightarrow (y+1)(y+2)(y^2-3y+11)=0$
Vậy PT có các nghiệm
$(x, y) \in \left\{ {(3,-1),(1,-2)} \right\}$
|
|
|
|
giải đáp
|
Bài toán hình chóp.
|
|
|
|
$MN$ không thể song song với $CD$ nên giả sử trong mp$(ABCD)$ nó cắt $CD$ tại điểm $I$.
$IP$ không thể song song với $SD$ nên giả sử trong mp$(SCD)$ nó cắt $SD$ tại điểm $J$.
Như vậy ta suy ra
giao tuyến của mp$(MNP)$ và mp$(ABCD)$ là $MN,$
giao tuyến của mp$(MNP)$ và mp$(SCD)$ là $IJ.$
Và rõ ràng hai giao tuyến này cắt nhau tại $I$ nằm trên $CD$.
|
|
|
|
giải đáp
|
Bài toán về về tứ diện.
|
|
|
|
Gọi $Q$ là trung điểm của $AD$.
Theo tính chất đường trung bình ta có
$MQ \parallel BD, MQ = \frac{1}{2}BD$.
Mặt khác thì cũng có
$NP \parallel BD, NP = \frac{1}{2}BD$.
suy ra
$NP \parallel MQ, NP =MQ$.
Điều này chứng tỏ $M,N,P,Q$ đồng phẳng và hiển nhiên thấy thiết diện là hình bình hành $MNPQ$.
|
|
|
|