|
|
giải đáp
|
giai giup em bai nay^^
|
|
|
|
Áp dụng BĐT Cô-si ta có
$2BC+BD \ge 2\sqrt{2BC.BD}=2\sqrt{2BA^2}=2\sqrt{8R^2}=4R\sqrt 2$.
Vậy $\min (2BC+BD)=4R\sqrt 2\Leftrightarrow 2BC=BD\Leftrightarrow C$ là trung điểm của $BD\Leftrightarrow AC=CB$
|
|
|
|
giải đáp
|
hệ phương trình có số mũ lớn
|
|
|
|
Từ PT thứ nhất ta suy ra
$\begin{cases}0\le x^2 \le 1 \\ 0\le y^2 \le 1 \end{cases}\Leftrightarrow \begin{cases}0\le x^{10} \le x^8 \\ 0\le y^{10} \le y^8 \end{cases}\Rightarrow x^{10}+y^{10} \le x^8+y^8$
Như vậy kết hợp với PT thứ hai ta phải có
$\begin{cases}x^{10}= x^8 \\ y^{10} = y^8\\x^2+y^2=1 \end{cases}\Leftrightarrow (x,y) \in \left\{ {(0,\pm1), (\pm1,0)} \right\}$
|
|
|
|
giải đáp
|
Một số bài toán Ôn tập về Xác suất - Nhị thức Newton.
|
|
|
|
3.
a) Trong $1000$ số từ $0$ đến $999$ có $334$ số chia hết cho $3$, có dạng $3k, 0\le k \le 333$.
Suy ra xác suất cần tìm là $\frac{334}{1000}$
a) Trong $1000$ số từ $0$ đến $999$ có $200$ số chia hết cho $5$, có dạng $5k, 0\le k \le 199$.
Suy ra xác suất cần tìm là $\frac{200}{1000}=\frac{1}{5}$
|
|
|
|
|
|
giải đáp
|
KHA KHO
|
|
|
|
Điều kiện $x \ne -2$.
Loga cơ số $2$ hai vế ta được PT
$\Leftrightarrow \frac{3x}{x+2}=\log_2 36+(2-x)\log_23$
$\Leftrightarrow 3x=\log_2 36(x+2)+(2-x)(x+2)\log_23$
$\Leftrightarrow 3x=\log_2 36(x+2)+(2-x)(x+2)\log_23$
$\Leftrightarrow 3x=\log_2 36(x+2)+(4-x^2)\log_23$
$\Leftrightarrow x^2\log_23+x(3-\log_2 36)-(2\log_2 36+4\log_23)=0$
Pt này có $\Delta =(3-\log_2 36)^2+4\log_23(2\log_2 36+4\log_23)$
Vậy Pt có nghiệm
$\displaystyle{x=\frac{\log_2 36-3\pm\sqrt{(3-\log_2 36)^2+4\log_23(2\log_2 36+4\log_23)}}{2\log_23}}$
|
|
|
|
giải đáp
|
cho 3 số
|
|
|
|
Ta có
$ \frac {a^2 +b^2}{a +b} = \frac {a +b}{2} +\frac {(a
-b)^2}{2(a +b)} \ge \frac {a +b}{2} +\frac {(a -b)^2}{2(a +b +c)}$
suy ra
$\sum \frac {a^2 +b^2}{a +b} \ge (a +b +c) +\frac {a^2 +b^2 +c^2 -(ab +bc +ca)}{a +b +c}$
Ta cần chứng minh
$ (a +b +c) +\frac {a^2 +b^2 +c^2 -(ab +bc +ca)}{a +b +c}
\ge 3 $
$\iff$$ 2(a^2 +b^2 +c^2) +(ab +bc +ca) \ge 3(a +b +c) =\sqrt {3(a^2
+b^2 +c^2)}(a +b +c)$
$\iff$$ \frac {(a +b +c)^2 +3(a^2 +b^2 +c^2)}{2} \ge \sqrt {3(a^2 +b^2
+c^2)}(a +b +c)$
nhưng đây là điều hiển nhiên đúng vì theo BĐT Cô-si.
|
|
|
|
giải đáp
|
giải pt
|
|
|
|
Ta có
$\sqrt{2x^{2}-2x+5}=\sqrt{2\left ( x-\frac{1}{2} \right )^2+\frac{9}{2}} \ge \frac{3}{\sqrt 2}$
$\sqrt{2x^{2}-6x+9}=\sqrt{2\left ( x-\frac{3}{2} \right )^2+\frac{9}{2}} \ge \frac{3}{\sqrt 2}$
Suy ra
$\sqrt{2x^{2}-2x+5}+\sqrt{2x^{2}-6x+9} \ge 3\sqrt 2 >4$
Như vậy PT đã cho vô nghiệm.
|
|
|
|
giải đáp
|
chứng minh nào
|
|
|
|
Ta có
$\sum_{k=0}^{n}(3k+1)=3\sum_{k=0}^{n}k+n+1=3\frac{n(n+1)}{2}+n+1=\frac{(n+1)(3n+2)}{2}$
$\sum_{k=0}^{n}(2k+3)=2\sum_{k=0}^{n}k+3(n+1)=2\frac{n(n+1)}{2}+3(n+1)=(n+1)(n+3)$
Do đó
$a_n=\frac{3n+2}{2(n+3)}\Rightarrow \mathop {\lim }\limits_{n \to +\infty}a_n=\frac{3}{2}$
|
|
|
|
giải đáp
|
Bài 100425
|
|
|
|
c) Hai điều sau đây là hiển nhiên đúng
$\begin{cases}(x+1)^2 \ge 0 \\(x-1)^2 \ge 0 \end{cases}\Leftrightarrow \begin{cases}x^2+1 \ge -2x \\x^2+1 \ge 2x\end{cases}\Leftrightarrow -1 \le \frac{2x}{x^2+1} \le 1$
như vậy ta luôn có $-1 \le \frac{2x}{x^2+1} \le 1$ với mọi $x$ nên tập xác định của hàm
$y = \arccos \frac{2x}{x^2+1} $ là với mọi $x \in \mathbb{R}.$
|
|
|
|
giải đáp
|
Bài 100425
|
|
|
|
b) Nếu $u=\arcsin x\Rightarrow x=\sin u$. Mà $-1 \le \sin u \le 1 $ nên điều kiện cho $x$ là $-1 \le x \le 1$.
Với $y=\arcsin^2 (x-1)$ thì ta cần
$-1 \le x-1 \le 1 \Leftrightarrow 0 \le x \le 2$.
|
|
|
|
giải đáp
|
Bài 100425
|
|
|
|
a) Nếu $u=\arccos x\Rightarrow x=\cos u$. Mà $-1 \le \cos u \le 1 $ nên điều kiện cho $x$ là $-1 \le x \le 1$.
Với $y=\arccos (\frac{x}{3}-1)$ thì ta cần
$-1 \le \frac{x}{3}-1 \le 1 \Leftrightarrow 0 \le x \le 6$.
|
|
|
|
giải đáp
|
1 bạn ở fb hỏi
|
|
|
|
d. Để tìm các điểm trên Parabol cách đều hai trụ tọa độ, ta giải hai hệ
$(I) \begin{cases}y=2x^2 \\ y=x \end{cases}\Rightarrow x=2x^2\Leftrightarrow\left[ {\begin{matrix} x=0\\x=\frac{1}{2} \end{matrix}} \right.\Leftrightarrow (x,y) \in \left\{ {(0,0); (\frac{1}{2},\frac{1}{2})} \right\} $
$(II) \begin{cases}y=2x^2 \\ y=-x \end{cases}\Rightarrow
-x=2x^2\Leftrightarrow\left[ {\begin{matrix} x=0\\x=-\frac{1}{2}
\end{matrix}} \right.\Leftrightarrow (x,y) \in \left\{ {(0,0);
(-\frac{1}{2},-\frac{1}{2})} \right\} $
Vậy có ba điểm thỏa mãn yêu cầu bài toán là $(0,0), (\frac{1}{2},\frac{1}{2})$ và $ (-\frac{1}{2},-\frac{1}{2})$.
|
|
|
|
giải đáp
|
1 bạn ở fb hỏi
|
|
|
|
c. Để tìm các điểm trên Parabol có tung độ bằng $y=4$ ta giải Pt
$4=2x^2\Leftrightarrow x^2=2\Leftrightarrow x = \pm \sqrt 2$.
Vậy có hai điểm thỏa mãn yêu cầu bài toán là $(\sqrt 2,4)$ và $(-\sqrt 2,4)$.
|
|
|
|
giải đáp
|
1 bạn ở fb hỏi
|
|
|
|
b. PT parabol $y=2x^2$ có điểm thấp nhất là gốc tọa độ $O(0,0)$, trụ đối xứng là trục tung $Oy$. 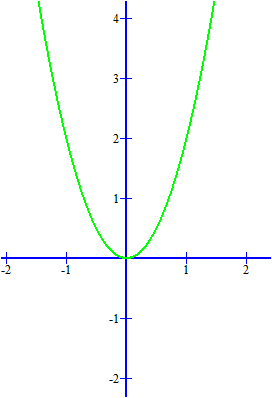 |
|
|
|
giải đáp
|
1 bạn ở fb hỏi
|
|
|
|
a. Tọa độ điểm $A(-1;2)$ thỏa mãn PT Parabol nên
$2=a.(-1)^2\Leftrightarrow a=2$
|
|