Lời giải này có yêu cầu trả vỏ sò để xem. Bạn hãy link trên để vào xem chi tiết

Lời giải này có yêu cầu trả vỏ sò để xem. Bạn hãy link trên để vào xem chi tiết

$I = \int_{\frac{\pi}{3}}^{\frac{2\pi}{3}} \frac{x + (x + \sin x)\sin x}{\sin^2 x (1 + \sin x)} dx$
$I = \int_{\frac{\pi}{3}}^{\frac{2\pi}{3}} \frac{x}{\sin^2 x}dx+ \int_{\frac{\pi}{3}}^{\frac{2\pi}{3}} \frac{1}{1 + \sin x} dx$

$I=I_1+I_2$
Trong đó
$I_1=\int\limits_{\frac{\pi}{3}}^{\frac{2\pi}{3}} \frac{xdx}{\sin^2x}=\int\limits_{\frac{\pi}{3}}^{\frac{2\pi}{3}} \left (\cot x -\cot x+ \frac{x}{\sin^2x} \right )dx$
 $= \int\limits_{\frac{\pi}{3}}^{\frac{2\pi}{3}} \cot xdx- \int\limits_{\frac{\pi}{3}}^{\frac{2\pi}{3}} \left (\cot x- \frac{x}{\sin^2x} \right )dx$
$= \int\limits_{\frac{\pi}{3}}^{\frac{2\pi}{3}} \frac{d(\sin x)}{\sin x}- \int\limits_{\frac{\pi}{3}}^{\frac{2\pi}{3}} \left (x\cot x \right )'dx$
 $=\left[ {\ln |\sin x|-x\cot x} \right]_{\frac{\pi}{3}}^{\frac{2\pi}{3}} $
 $=\displaystyle{\frac{1}{\sqrt 3}\pi}$

$I_2= \int_{\frac{\pi}{3}}^{\frac{2\pi}{3}} \frac{1}{1 + \sin x} dx$
$=2 \int_{\frac{\pi}{3}}^{\frac{2\pi}{3}} \frac{(\sin\frac{x}{2}+\cos \frac{x}{2})(\sin\frac{x}{2})'-(\sin\frac{x}{2}+\cos \frac{x}{2})'(\sin\frac{x}{2})}{(\sin\frac{x}{2}+\cos \frac{x}{2})^2} dx$
$=2 \int_{\frac{\pi}{3}}^{\frac{2\pi}{3}} \left ( \frac{\sin\frac{x}{2}}{\sin\frac{x}{2}+\cos \frac{x}{2}} \right )' dx$
$=\left[ {   2\frac{\sin\frac{x}{2}}{\sin\frac{x}{2}+\cos \frac{x}{2}}   } \right]_{\frac{\pi}{3}}^{\frac{2\pi}{3}} $
$4-2\sqrt 3$

Vậy $\boxed{I=\frac{1}{\sqrt 3}\pi+4-2\sqrt 3}$

Ta có
$ \sum_{cyc} \frac{a^2}{b} - \sum_{sym} a = \sum_{cyc}( \frac{a^2}{b} + b-2a ) = \sum_{cyc} \frac{(a-b)^2}{b}  $
Ta cần chứng minh
$\sum_{cyc} \frac{(a-b)^2}{b} - \frac{4(a-b)^2}{a+b+c} \ge 0 $
$ \Leftrightarrow S_c(a-b)^2+S_a(b-c)^2+S_b(c-a)^2 \ge 0 $
Trong đó
$
\begin{cases}
S_a = \frac{1}{c} \\
S_b = \frac{1}{a} \\
S_c = \frac{1}{b} - \frac{4}{a+b+c}
\end{cases}
$
Bằng phương pháp SOS ta cần kiểm tra
$
\begin{cases}
S_b \ge 0 \\
S_b +S_c \ge 0 \\
S_b + S_a \ge 0
\end{cases}
$
Và ta chỉ cần kiểm tra
$ S_b +S_c=  \frac{1}{a}+\frac{1}{b} - \frac{4}{a+b+c} \ge \frac{4}{a+b} - \frac{4}{a+b+c} \ge 0 $.
Vậy ta có đpcm.

$I=\int\limits_{\frac{\pi}{4}}^{\frac{\pi}{3}}\frac{xdx}{\sin^2x}=\int\limits_{\frac{\pi}{4}}^{\frac{\pi}{3}}\left (\cot x -\cot x+ \frac{x}{\sin^2x} \right )dx$
 $= \int\limits_{\frac{\pi}{4}}^{\frac{\pi}{3}}\cot xdx- \int\limits_{\frac{\pi}{4}}^{\frac{\pi}{3}}\left (\cot x- \frac{x}{\sin^2x} \right )dx$
$= \int\limits_{\frac{\pi}{4}}^{\frac{\pi}{3}}\frac{d(\sin x)}{\sin x}- \int\limits_{\frac{\pi}{4}}^{\frac{\pi}{3}}\left (x\cot x \right )'dx$
 $=\left[ {\ln |\sin x|-x\cot x} \right]_{\frac{\pi}{4}}^{\frac{\pi}{3}} $
 $=\boxed{\displaystyle{\frac{9-4\sqrt 3}{36}\pi+\frac{1}{2}\ln\frac{3}{2}}}$

Dễ thấy rằng với mọi $n$ thì $x_n \in [-1,1].$
Tiếp theo ta chứng minh $\cos x$ là hàm co, dễ thấy vì theo định lý Lagrange
$|\cos x_1 - \cos x_2|=|\sin c||x_1-x_2| \le |x_1-x_2|$ với $c \in (x_1,x_2).$
Như vậy với bất kỳ điểm xuất phát $x_0$ nào thì quá trình lặp đều hội tụ tới điểm $\xi$ duy nhất sao cho $\xi=\cos \xi$.
Việc chứng minh PT $a=\cos a$ có nghiệm duy nhất là một điều không phức tạp.

b.
Khi $SA=SC=a$ thì tam giác $SBC$ đều nên $\alpha=60^\circ.$
Từ câu a suy ra $\sin \varphi=\frac{\sqrt 2}{\sqrt 3}\Rightarrow IO=\frac{1}{2}SO=\frac{1}{2}SC\sin\varphi=\frac{1}{\sqrt 6}a$
Lại có $OC=\frac{1}{\sqrt 3}a$, theo Py-ta-go thì $IC=\sqrt{OC^2+IO^2}=\frac{1}{\sqrt 2}a$
Ta có $IA=IB=IC=\frac{1}{\sqrt 2}a, AB=AC=BC=a$ nên các tam giác $IAB, IAC, IBC$ vuông tại $I$.
Vậy ta có đpcm.

a.
Kẻ $SO \perp mp(ABC)$ thì $O$ là tâm của tam giác đều $ABC$.
Khi đó $\varphi = \widehat{OCS}.$
Mặt khác trong tam giác cân $SBC$ tại $S$, kẻ đường cao $SH$ thì dễ thấy $SC=\frac{HC}{\sin\widehat{HSC}}=\frac{a}{2\sin\frac{\alpha}{2}}$
Như vậy, $\cos \varphi=\frac{OC}{SC}=\frac{\frac{a}{\sqrt 3}}{\frac{a}{2\sin\frac{\alpha}{2}}}=\frac{2}{\sqrt 3}\sin\frac{\alpha}{2}$
Vậy $\sin \varphi=\sqrt{1-\frac{4}{3}\sin^2\frac{\alpha}{2}}$

Giả sử hình $H$ có hai trục đối xứng đó là $Ox, Oy$ vuông góc với nhau tại $O$.
Xét điểm $A \in H$.
Xét các phép đối xứng
$Đ_{Ox} : A \to A_1\Rightarrow \begin{cases}OA=OA_1 \\ \widehat{AOx}= \widehat{A_1Ox}= \frac{1}{2}\widehat{A_1OA}\\A_1 \in H \end{cases}$
$Đ_{Oy} : A_1 \to A_2\Rightarrow \begin{cases}OA_2=OA_1 \\ \widehat{A_2Oy}= \widehat{A_1Oy}= \frac{1}{2}\widehat{A_1OA_2}\\A_2 \in H \end{cases}$
Từ hai điều này suy ra
$ \begin{cases}OA_2=OA \\ \widehat{AOA_2}= \widehat{AOA_1}+ \widehat{A_2OA_1}= 2 \widehat{A_1Ox}+ 2 \widehat{A_1Oy}= \widehat{yOx}=180^\circ\\A, A_2 \in H \end{cases}$
Từ đây suy ra có một phép đối xứng tâm cho mọi điểm thuộc hình $H$. Tức là hình $H$ có tâm đối xứng, đpcm.

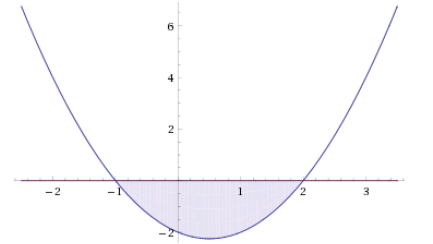Khảo sát sự biến thiên và vẽ đồ hàm số $y=x^2-x-2$ ta được đây là Parabol có đỉnh thấp nhất là điểm $I(1/2, -9/4)$. Giao điểm với trục hoành lần lượt là $(-1,0), (2,0).$
Để tìm $y<0$ chỉ cần nhìn vào đồ thị và lấy $-1<x<2$.

Giả sử $x$ là nghiệm nguyên của PT, khi đó ta có:
$\cos \left[ {\frac{\pi }{10}\left( {3x - \sqrt {9{x^2} + 80x -40} } \right)} \right] = 1$
$\Leftrightarrow \frac{\pi }{10}\left( {3x - \sqrt {9{x^2} + 80x -40} } \right) = k2\pi $ ($k \in \mathbb{Z}$)
$\Leftrightarrow \sqrt {9{x^2} + 80x -40}  = 3x - 20k$
$   \Leftrightarrow \left\{ \begin{array}
  3x - 20k \ge 0  \\
  9{x^2} + 80x -40 = \left( {3x - 20k} \right)^2\end{array}  \right. $
$ \Leftrightarrow \left\{ \begin{array}
  3x- 20k \ge 0  \\
  x = \frac{{10{k^2} +1}}{{3k + 2}}  \\
\end{array}  \right.$
$ \Leftrightarrow \left\{ \begin{array}
  3x - 20k \ge 0  \\
  9x = 30k - 20 + \frac{{49}}{{3k + 2}}  \\
\end{array}  \right.$                    $\left( 1\right)$
$ \Rightarrow \frac{{49}}{{3k + 2}} \in \mathbb{Z}$, suy ra :$k \in \left\{ {{\text{-17,-3; - 1}}} \right\}$  $\left(2 \right)$
Từ  $\left( 2 \right)$ , bằng cách thử trực tiếp vào$\left( 1 \right)$ ta được:
          $\left[ \begin{array}
  \left\{ \begin{array}
  k =  -1  \\
  x =  - 11  \\
\end{array}  \right. &\textrm{(loại)} \\
  \left\{ \begin{array}
  k =  - 17  \\
  x =  - 59  \\
\end{array}  \right.  \\
\left\{ \begin{array}
  k =  - 3  \\
  x =  - 13  \\
\end{array}\right.
\end{array}  \right.$
Vậy: $x\in\{-13,-59\}$

      $6\sin x\cos^2x\cos2x+\sin^3x=0$
$\Leftrightarrow \sin x\left (6 \cos^2x\cos2x+\sin^2x \right )=0$
$\Leftrightarrow \sin x\left[ {3(1+\cos2x)\cos2x+\frac{1-\cos2x}{2}} \right]=0$
$\Leftrightarrow \sin x\left[ {6\cos^22x+5\cos2x+1} \right]=0$
$\Leftrightarrow \sin x\left(3\cos2x+1\right)\left(2\cos2x+1\right)=0$.

b)
$B= \mathop {\lim }\limits_{n\to \infty }\frac{(n+2)!+ (n+1)!}{ (n+2)!- (n+1)! }= \mathop {\lim }\limits_{n\to \infty }\frac{(n+1)!(n+2+1) }{ (n+1)!(n+2-1)  }   = \mathop {\lim }\limits_{n\to \infty }\frac{n+3 }{n+1  } = \mathop {\lim }\limits_{n\to \infty }\frac{1+\frac{3}{n} }{1+\frac{1}{n}  }  =1  $

a)
$A=\mathop {\lim }\limits_{n\to \infty }\frac{(n+1)^4- (n-1)^4}{ (n+1)^4+ (n-1)^4 }=\mathop {\lim }\limits_{n\to \infty }\frac{ 4n^3+4n}{ n^4+6n^2+1 }=\mathop {\lim }\limits_{n\to \infty }\frac{ \frac{4}{n} +\frac{4}{n^3} }{ 1+\frac{6}{n^2}+\frac{1}{n^4} }=\frac{0}{1}=0$

Lời giải này có yêu cầu trả vỏ sò để xem. Bạn hãy link trên để vào xem chi tiết