|
|
bình luận
|
giải pt
Hãy ấn chữ V dưới đáp án để chấp nhận nếu như bạn thấy lời giải này chính xác, và nút mũi tên màu xanh để vote up nhé. Thanks!
|
|
|
|
|
|
|
|
giải đáp
|
giải pt
|
|
|
|
Điều kiện $\begin{cases}x \ge -1 \\ x^{2}+x-3>0\end{cases}$ PT $\Leftrightarrow x^{2}+x-3=3\sqrt{x^{3}+1}$ $\Leftrightarrow (x^{2}+x-3)^2=9(x^{3}+1)$ $\Leftrightarrow x^4-7x^3-5x^2-6x=0$ $\Leftrightarrow x^3-7x^2-5x-6=0$ PT bậc ba này không có nghiệm đẹp. Để xem cách giải PT bậc ba tổng quát bạn có thể tham khảo phương pháp Cardano trên Google nhé. Pt có nghiệm duy nhất 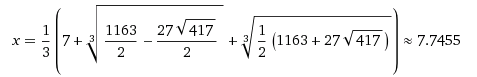 |
|
|
|
bình luận
|
bài nữa rùi đi ăn cơm này.hehe
Hãy ấn chữ V dưới đáp án để chấp nhận nếu như bạn thấy lời giải này chính xác, và nút mũi tên màu xanh để vote up nhé. Thanks!
|
|
|
|
|
|
|
|
giải đáp
|
bài nữa rùi đi ăn cơm này.hehe
|
|
|
|
Giả sử rằng PT có nghiệm thì tất cả các biểu thức trong căn phải không âm.
Ta sẽ chứng minh điều sau
$$\sqrt{x+\sqrt{x^2-x+1} }<\sqrt{x+1+\sqrt{x^2+x+1} }+1$$
với mọi $x$ là cho các biểu thức có nghĩa.
Thật vậy,
+ Xét $x \ge 0$ thì hiển nhiên có
$0 < x^2-x+1 \le x^2+x+1$
$\Leftrightarrow x+\sqrt{x^2-x+1}<x+1+\sqrt{x^2+x+1}$
$\Leftrightarrow \sqrt{x+\sqrt{x^2-x+1} }<\sqrt{x+1+\sqrt{x^2+x+1} }+1$
+ Xét $x < 0$ thì
$0 < x^2-x+1 < x^2-2x+1=(1-x)^2$
$\Leftrightarrow \sqrt{x^2-x+1}<1-x$
$\Leftrightarrow x+\sqrt{x^2-x+1}<1$
$\Leftrightarrow \sqrt{x+\sqrt{x^2-x+1} }<\sqrt{x+1+\sqrt{x^2+x+1} }+1$
Tóm lại PT đã cho vô nghiệm.
|
|
|
|
|
|
giải đáp
|
bài tiếp nhé, mọi người cùng tham gia
|
|
|
|
Điều kiện $x > 2.$
PT
$\Leftrightarrow \sqrt[4]{\dfrac{x-1}{x-2}}+4m+(m+3) \sqrt[4]{\dfrac{x-2}{x-1}}=0$
Đặt $t= \sqrt[4]{\dfrac{x-1}{x-2}}>1$, thì PT
$\Leftrightarrow t+4m+(m+3)\dfrac{1}{t}=0\Leftrightarrow m(4+\dfrac{1}{t})=-\dfrac{3}{t}-t$
$\Leftrightarrow m=f(t)=\dfrac{-3-t^2}{4t+1}$
Lập bảng biến thiên của $f(t)$ trên $t>1$ ta suy ra $m <f(1)=-\dfrac{4}{5}$
|
|
|
|
bình luận
|
giải nhé moij người
Hãy ấn chữ V dưới đáp án để chấp nhận nếu như bạn thấy lời giải này chính xác, và nút mũi tên màu xanh để vote up nhé. Thanks!
|
|
|
|
|
|
|
|
giải đáp
|
giải nhé moij người
|
|
|
|
Điều kiện $x \ge 1.$
PT
$\Leftrightarrow m= \dfrac{-3\sqrt{x-1}+2\sqrt[4]{x^2-1}}{\sqrt{x+1}}=-3\sqrt{\dfrac{x-1}{x+1}}+2\sqrt[4]{\dfrac{x-1}{x+1}}$
Đặt $\begin{cases}t=\sqrt[4]{\dfrac{x-1}{x+1}}\Rightarrow 0 \le x <1 \\ m=f(t)=-3t^2+2t \end{cases}$
Lập bảng biến thiên của hàm $f(t)=-3t^2+2t$ trên $0 \le x <1$ ta có
$\underbrace{-1}_{\min_{[0,1)} f(t) } < f(t) \le \underbrace{\dfrac{1}{3}}_{\max_{[0,1)} f(t) }\Leftrightarrow \boxed{-1 < m \le\dfrac{1}{3} }$
|
|
|
|
bình luận
|
toan 9
Hãy ấn chữ V dưới đáp án để chấp nhận nếu như bạn thấy lời giải này chính xác, và nút mũi tên màu xanh để vote up nhé. Thanks!
|
|
|
|
|
|
|
|
giải đáp
|
toan 9
|
|
|
|
Bạn xem tại đây nhé
http://toan.hoctainha.vn/Hoi-Dap/Cau-Hoi/114779/tinh-tong
|
|
|
|
bình luận
|
bài này!!!
Hãy ấn chữ V dưới đáp án để chấp nhận nếu như bạn thấy lời giải này chính xác, và nút mũi tên màu xanh để vote up nhé. Thanks!
|
|
|
|
|
|
|
|
bình luận
|
Giải bất phương trình
Hãy ấn chữ V dưới đáp án để chấp nhận nếu như bạn thấy lời giải này chính xác, và nút mũi tên màu xanh để vote up nhé. Thanks!
|
|
|
|
|
|
|
|
giải đáp
|
bài này!!!
|
|
|
|
Điều kiện $x \ge 0.$
Hiển nhiên có các bđt sau
$\begin{cases}x^2+1 \ge 2x\\ x^6+x^4 \ge 2x^5 \end{cases}\Rightarrow x^6+x^4+x^2+1 \ge 2(x^5+x)$
Đặt
$a=\sqrt{x^5+x^3+x}, b=\sqrt{x^2(x^2-x+1)}, c=\sqrt{(x^2+1)^3} $
Ta có
$(a+b)^2 \le 2(a^2+b^2) =2(x^5+x^4+x^2+x) \le x^6+x^4+x^2+1+2x^4+2x^2=(x^2+1)^3=c^2$
Như vậy với Điều kiện $x \ge 0$ ta luôn có
$(a+b)^2 \le c^2 \Leftrightarrow a+b \le c\Leftrightarrow a \le c-b$.
Vậy tập nghiệm của BPT là $x \ge 0.$
|
|
|
|
giải đáp
|
Giải bất phương trình
|
|
|
|
Điều kiện $x \ge 0.$
Hiển nhiên có các bđt sau
$\begin{cases}x^2+1 \ge 2x\\ x^6+x^4 \ge 2x^5 \end{cases}\Rightarrow x^6+x^4+x^2+1 \ge 2(x^5+x)$
Đặt
$a=\sqrt{x^5+x^3+x}, b=\sqrt{x^2(x^2-x+1)}, c=\sqrt{(x^2+1)^3} $
Ta có
$(a+b)^2 \le 2(a^2+b^2) =2(x^5+x^4+x^2+x) \le x^6+x^4+x^2+1+2x^4+2x^2=(x^2+1)^3=c^2$
Như vậy với Điều kiện $x \ge 0$ ta luôn có
$(a+b)^2 \le c^2 \Leftrightarrow a+b \le c\Leftrightarrow a \le c-b$.
Vậy tập nghiệm của BPT là $x \ge 0.$
|
|
|
|
bình luận
|
Giải hệ phương trình
Hãy ấn chữ V dưới đáp án để chấp nhận nếu như bạn thấy lời giải này chính xác, và nút mũi tên màu xanh để vote up nhé. Thanks!
|
|
|
|
|
|