|
|
bình luận
|
1 bạn ở fb hỏi
Hãy ấn chữ V dưới đáp án để chấp nhận nếu như bạn thấy lời giải này chính xác, và nút mũi tên màu xanh để vote up nhé. Thanks!
|
|
|
|
|
|
|
|
giải đáp
|
1 bạn ở fb hỏi
|
|
|
|
d. Để tìm các điểm trên Parabol cách đều hai trụ tọa độ, ta giải hai hệ
$(I) \begin{cases}y=2x^2 \\ y=x \end{cases}\Rightarrow x=2x^2\Leftrightarrow\left[ {\begin{matrix} x=0\\x=\frac{1}{2} \end{matrix}} \right.\Leftrightarrow (x,y) \in \left\{ {(0,0); (\frac{1}{2},\frac{1}{2})} \right\} $
$(II) \begin{cases}y=2x^2 \\ y=-x \end{cases}\Rightarrow
-x=2x^2\Leftrightarrow\left[ {\begin{matrix} x=0\\x=-\frac{1}{2}
\end{matrix}} \right.\Leftrightarrow (x,y) \in \left\{ {(0,0);
(-\frac{1}{2},-\frac{1}{2})} \right\} $
Vậy có ba điểm thỏa mãn yêu cầu bài toán là $(0,0), (\frac{1}{2},\frac{1}{2})$ và $ (-\frac{1}{2},-\frac{1}{2})$.
|
|
|
|
bình luận
|
1 bạn ở fb hỏi
Hãy ấn chữ V dưới đáp án để chấp nhận nếu như bạn thấy lời giải này chính xác, và nút mũi tên màu xanh để vote up nhé. Thanks!
|
|
|
|
|
|
|
|
bình luận
|
1 bạn ở fb hỏi
Hãy ấn chữ V dưới đáp án để chấp nhận nếu như bạn thấy lời giải này chính xác, và nút mũi tên màu xanh để vote up nhé. Thanks!
|
|
|
|
|
|
|
|
bình luận
|
1 bạn ở fb hỏi
Hãy ấn chữ V dưới đáp án để chấp nhận nếu như bạn thấy lời giải này chính xác, và nút mũi tên màu xanh để vote up nhé. Thanks!
|
|
|
|
|
|
|
|
giải đáp
|
1 bạn ở fb hỏi
|
|
|
|
c. Để tìm các điểm trên Parabol có tung độ bằng $y=4$ ta giải Pt
$4=2x^2\Leftrightarrow x^2=2\Leftrightarrow x = \pm \sqrt 2$.
Vậy có hai điểm thỏa mãn yêu cầu bài toán là $(\sqrt 2,4)$ và $(-\sqrt 2,4)$.
|
|
|
|
giải đáp
|
1 bạn ở fb hỏi
|
|
|
|
b. PT parabol $y=2x^2$ có điểm thấp nhất là gốc tọa độ $O(0,0)$, trụ đối xứng là trục tung $Oy$. 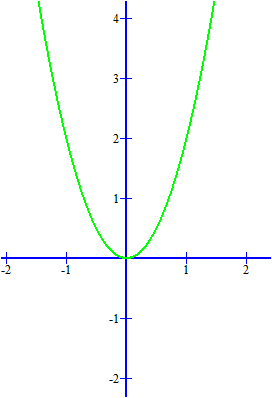 |
|
|
|
giải đáp
|
1 bạn ở fb hỏi
|
|
|
|
a. Tọa độ điểm $A(-1;2)$ thỏa mãn PT Parabol nên
$2=a.(-1)^2\Leftrightarrow a=2$
|
|
|
|
|
|
|
|
giải đáp
|
cho lăng trụ đứng ABCA'B'C' có tất cả các cạnh bằng a
|
|
|
|
a)
Xét lăng trụ $ABC.A'B'C'$ và chóp tam giác $C'.ABC$ có chung mặt đáy $ABC$ và đường cao $CC'$ nên
$$V_{C'.ABC}=\frac{1}{3}V_{ABC.A'B'C'}$$
Lý luận tương tự cũng có $$V_{A.A'B'C'}=\frac{1}{3}V_{ABC.A'B'C'}$$
Vậy
$$V_{ABB'C}=V_{ABC.A'B'C'}-V_{C'.ABC}-V_{A.A'B'C'}=\frac{1}{3}V_{ABC.A'B'C'}=\frac{1}{3}AA'.S_{A'B'C'}=\frac{1}{3}.a.\frac{a^2\sqrt 3}{4}=\frac{a^3\sqrt 3}{12}$$
|
|
|
|
bình luận
|
bài nữa nhá
Hãy ấn chữ V dưới đáp án để chấp nhận nếu như bạn thấy lời giải này chính xác, và nút mũi tên màu xanh để vote up nhé. Thanks!
|
|
|
|
|
|
|
|
giải đáp
|
bài nữa nhá
|
|
|
|
Điều kiện $\sin x \ne \frac{\sqrt 3 }{2}, \sin x \ne 0, \cos x \ne 0$.
PT
$\Leftrightarrow 4\cos 3x.\cos x - 2\cos 4x - 4\cos x + \tan\frac{x}{2}.\tan x + 2=0$
$\Leftrightarrow 2\left (\cos 4x+\cos 2x \right ) - 2\cos 4x - 4\cos x + \tan\frac{x}{2}.\tan x + 2=0$
$\Leftrightarrow 2\left (1+\cos 2x \right ) - 4\cos x + \tan\frac{x}{2}.\tan x =0$
$\Leftrightarrow 4\cos^2 x - 4\cos x + \tan\frac{x}{2}.\tan x =0$
$\Leftrightarrow \tan\frac{x}{2}.\tan x =4\cos x(1-\cos x)$
$\Leftrightarrow \tan\frac{x}{2}.\tan x =8\cos x. \sin^2 \frac{x}{2}$
$\Leftrightarrow \sin\frac{x}{2}.\sin x =8\cos^2 x .\sin^2 \frac{x}{2}.\cos \frac{x}{2}$
$\Leftrightarrow \sin\frac{x}{2}.\sin x =4\cos^2 x .\sin \frac{x}{2}. \sin x$
$\Leftrightarrow1 =4\cos^2 x$
$\Leftrightarrow \cos x =\pm \frac{1}{2}$ và do $\sin x \ne \frac{\sqrt 3 }{2}$ nên
$\Leftrightarrow \left[ {\begin{matrix} x=-\frac{\pi}{3}+k2\pi\\ x=-\frac{2\pi}{3}+k2\pi \end{matrix}} \right. (k \in \mathbb{Z})$
|
|
|
|
bình luận
|
giải pt lượng giác
Hãy ấn chữ V dưới đáp án để chấp nhận nếu như bạn thấy lời giải này chính xác, và nút mũi tên màu xanh để vote up nhé. Thanks!
|
|
|
|
|
|
|
|
giải đáp
|
giải pt lượng giác
|
|
|
|
Điều kiện $\sin x \ne 1, \cos x \ne 0.$
PT
$\Leftrightarrow \frac{1 + \cos^2 x}{2(1 - \sin x)} - \frac{1}{2}(1 + \sin x) = \tan^2 x+ \tan^2 x.\sin x $
$\Leftrightarrow \frac{1 + \cos^2 x-(1 - \sin^2 x) }{2(1 - \sin x)} = \tan^2 x(1+\sin x )$
$\Leftrightarrow \frac{1 }{2(1 - \sin x)} = \tan^2 x(1+\sin x )$
$\Leftrightarrow \frac{1 }{2} = \tan^2 x(1 - \sin^2 x)$
$\Leftrightarrow \frac{1 }{2} = \tan^2 x\cos^2 x$
$\Leftrightarrow \frac{1 }{2} =\sin^2 x$
$\Leftrightarrow \sin x = \pm \frac{1}{\sqrt 2}$
Đến đây quá đơn giản để tìm nghiệm :)
|
|