a. $\textbf{Cách 2}$
hiển nhiên có $\cos 30 =\frac{\sqrt 3}{2}\Rightarrow 2\cos^2 15 -1 =\frac{\sqrt 3}{2}\Rightarrow \cos^2 15=\frac{2+\sqrt 3}{4}$
Do $\cos 15 > 0\Rightarrow \cos 15= \frac{{\sqrt {2 + \sqrt 3 } }}{2} = \frac{{1 + \sqrt 3 }}{{2\sqrt 2 }}$

a.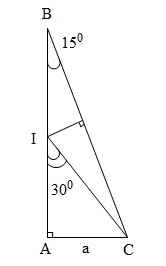

Xét $\Delta ABC$ vuông tại $A$ có $\widehat B = {15^\circ}$
Kẻ trung trực của $BC$ cắt $AB$ tại $I$.
Ta có $\widehat {AIC} = {30^\circ}$. Đặt $AC = a$
Thì $\left\{ \begin{array}{l}
IB = IC = \frac{a}{\sin 30^\circ}=2a\\
AI = a\cot {30^\circ} = a\sqrt 3
\end{array} \right.$
    $ \Rightarrow AB = 2a + a\sqrt 3 $
Suy ra:
•    $c{\rm{o}}{{\rm{s}}^2}{15^\circ} = \frac{1}{{1 + \tan^2 {{15}^\circ}}} = \frac{1}{{8 - 4\sqrt 3 }}$ $ = \frac{{2 + \sqrt 3 }}{4}$
$ \Rightarrow c{\rm{os}}{15^\circ} = \frac{{\sqrt {2 + \sqrt 3 } }}{2} = \frac{{1 + \sqrt 3 }}{{2\sqrt 2 }}$

b) Trong hệ thức Stewart nếu $AM$ là đường trung tuyến thì $BM=CM=\frac{a}{2}$
Suy ra $aMA^2=\frac{a}{2}b^2+\frac{a}{2}c^2-\frac{a^3}{4}\Rightarrow MA^2=\frac{1}{2}b^2+\frac{1}{2}c^2-\frac{a^2}{4}$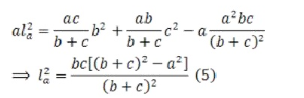



Điều này có nghĩa là
$AD=l_a=\frac{2}{b+c}\sqrt{bcp(p-a)}$

a)

Ta đã biết định lý hàm số  SIN
$\sin A =\frac{a}{2R}$,
định lý hàm số COS
$\cos A= \frac{b^2+c^2-a^2}{2bc}$
và công thức
$abc=4RS$
Vậy
$\tan A = \frac{\sin A}{\cos A}=\frac{2abc}{2R(b^2+c^2-a^2)}=\frac{4S}{b^2+c^2-a^2}$, đpcm.

      $ \cos \left[ {\frac{\pi }{2} - \pi \left( {{x^2} + 2x} \right)} \right] = \sin \left( {\pi {x^2}} \right)$
$ \Leftrightarrow \sin \left[ {\pi \left( {{x^2} + 2x} \right)} \right] = \sin \left( {\pi {x^2}} \right)$
$ \Leftrightarrow  \left[ {\begin{matrix} \pi \left( x^2 + 2x \right) = \pi x^2 + k2 \pi   \\ \pi (x^2 + 2x)  = \pi  - \pi x^2 + k2\pi \end{matrix}} \right.     $$ \Leftrightarrow \left[ {\begin{matrix} x = k \in \mathbb{Z}  \\ 2x^2 + 2x - \left( 2k + 1 \right) = 0  \end{matrix}} \right.  $$\left( {\text{*}} \right)$
Do $\begin{cases}\left( {\text{*}} \right)  \\x{\text{ > }}0  \\k \in \mathbb{Z}  \\\end{cases}  $   suy ra $x=\frac{-b +\sqrt{\Delta}}{2a}=\frac{-1 +\sqrt{4k+3}}{2}$
Để $x$ dương và nhỏ nhất với $k \in \mathbb{Z}$ và $4k+3 \ge 0$ thì cần $k=0.$
Vậy $\min x = \frac{{\sqrt 3  - 1}}{2}$

a)
Ta có
$\begin{cases}CD \parallel AB, CD=AB\\ EF \parallel AB, EF=AB \end{cases}\Rightarrow CD \parallel EF, CD=EF$
suy ra $DCEF$ là hình bình hành nên $DF \parallel CE$.
Ta có
$ OD \parallel O'F, OD=O'F$
suy ra $DOO'F$ là hình bình hành nên $DF \parallel OO'$.
Và ta có đpcm.