b.
Khi $SA=SC=a$ thì tam giác $SBC$ đều nên $\alpha=60^\circ.$
Từ câu a suy ra $\sin \varphi=\frac{\sqrt 2}{\sqrt 3}\Rightarrow IO=\frac{1}{2}SO=\frac{1}{2}SC\sin\varphi=\frac{1}{\sqrt 6}a$
Lại có $OC=\frac{1}{\sqrt 3}a$, theo Py-ta-go thì $IC=\sqrt{OC^2+IO^2}=\frac{1}{\sqrt 2}a$
Ta có $IA=IB=IC=\frac{1}{\sqrt 2}a, AB=AC=BC=a$ nên các tam giác $IAB, IAC, IBC$ vuông tại $I$.
Vậy ta có đpcm.

a.
Kẻ $SO \perp mp(ABC)$ thì $O$ là tâm của tam giác đều $ABC$.
Khi đó $\varphi = \widehat{OCS}.$
Mặt khác trong tam giác cân $SBC$ tại $S$, kẻ đường cao $SH$ thì dễ thấy $SC=\frac{HC}{\sin\widehat{HSC}}=\frac{a}{2\sin\frac{\alpha}{2}}$
Như vậy, $\cos \varphi=\frac{OC}{SC}=\frac{\frac{a}{\sqrt 3}}{\frac{a}{2\sin\frac{\alpha}{2}}}=\frac{2}{\sqrt 3}\sin\frac{\alpha}{2}$
Vậy $\sin \varphi=\sqrt{1-\frac{4}{3}\sin^2\frac{\alpha}{2}}$

Giả sử hình $H$ có hai trục đối xứng đó là $Ox, Oy$ vuông góc với nhau tại $O$.
Xét điểm $A \in H$.
Xét các phép đối xứng
$Đ_{Ox} : A \to A_1\Rightarrow \begin{cases}OA=OA_1 \\ \widehat{AOx}= \widehat{A_1Ox}= \frac{1}{2}\widehat{A_1OA}\\A_1 \in H \end{cases}$
$Đ_{Oy} : A_1 \to A_2\Rightarrow \begin{cases}OA_2=OA_1 \\ \widehat{A_2Oy}= \widehat{A_1Oy}= \frac{1}{2}\widehat{A_1OA_2}\\A_2 \in H \end{cases}$
Từ hai điều này suy ra
$ \begin{cases}OA_2=OA \\ \widehat{AOA_2}= \widehat{AOA_1}+ \widehat{A_2OA_1}= 2 \widehat{A_1Ox}+ 2 \widehat{A_1Oy}= \widehat{yOx}=180^\circ\\A, A_2 \in H \end{cases}$
Từ đây suy ra có một phép đối xứng tâm cho mọi điểm thuộc hình $H$. Tức là hình $H$ có tâm đối xứng, đpcm.

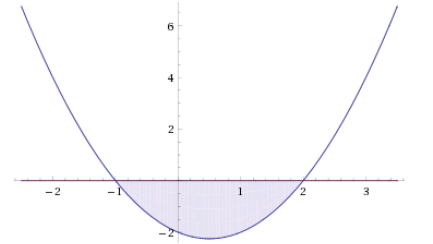Khảo sát sự biến thiên và vẽ đồ hàm số $y=x^2-x-2$ ta được đây là Parabol có đỉnh thấp nhất là điểm $I(1/2, -9/4)$. Giao điểm với trục hoành lần lượt là $(-1,0), (2,0).$
Để tìm $y<0$ chỉ cần nhìn vào đồ thị và lấy $-1<x<2$.

Giả sử $x$ là nghiệm nguyên của PT, khi đó ta có:
$\cos \left[ {\frac{\pi }{10}\left( {3x - \sqrt {9{x^2} + 80x -40} } \right)} \right] = 1$
$\Leftrightarrow \frac{\pi }{10}\left( {3x - \sqrt {9{x^2} + 80x -40} } \right) = k2\pi $ ($k \in \mathbb{Z}$)
$\Leftrightarrow \sqrt {9{x^2} + 80x -40}  = 3x - 20k$
$   \Leftrightarrow \left\{ \begin{array}
  3x - 20k \ge 0  \\
  9{x^2} + 80x -40 = \left( {3x - 20k} \right)^2\end{array}  \right. $
$ \Leftrightarrow \left\{ \begin{array}
  3x- 20k \ge 0  \\
  x = \frac{{10{k^2} +1}}{{3k + 2}}  \\
\end{array}  \right.$
$ \Leftrightarrow \left\{ \begin{array}
  3x - 20k \ge 0  \\
  9x = 30k - 20 + \frac{{49}}{{3k + 2}}  \\
\end{array}  \right.$                    $\left( 1\right)$
$ \Rightarrow \frac{{49}}{{3k + 2}} \in \mathbb{Z}$, suy ra :$k \in \left\{ {{\text{-17,-3; - 1}}} \right\}$  $\left(2 \right)$
Từ  $\left( 2 \right)$ , bằng cách thử trực tiếp vào$\left( 1 \right)$ ta được:
          $\left[ \begin{array}
  \left\{ \begin{array}
  k =  -1  \\
  x =  - 11  \\
\end{array}  \right. &\textrm{(loại)} \\
  \left\{ \begin{array}
  k =  - 17  \\
  x =  - 59  \\
\end{array}  \right.  \\
\left\{ \begin{array}
  k =  - 3  \\
  x =  - 13  \\
\end{array}\right.
\end{array}  \right.$
Vậy: $x\in\{-13,-59\}$