c) Trong phép quay tâm $O$ góc $90^\circ$ chiều dương là chiều ngược chiều kim đồng hồ thì điểm $O$ là điểm bất động.
Ta có
$Q_O(90^\circ) : A \to B$ vì $OA=OB$ và $\widehat{AOB}=90^\circ.$
$Q_O(90^\circ) : I \to P$ với $P$ là trung điểm của $BC$ vì $OI=OP$ và $\widehat{IOP}=90^\circ.$
Vậy $\triangle AIO \to \triangle BPO$ theo đúng thứ tự trên.

b) Trong phép vị tự tâm $A$ tỉ số $2$ thì điểm $A$ là điểm bất động.
Giả sử
$V_A^2 : I \to I'$ thì $\overrightarrow{AI}=2\overrightarrow{AI'}$ suy ra $I'$ là trung điểm của $AI$.
$V_A^2 : O \to O'$ thì $\overrightarrow{AO}=2\overrightarrow{AO'}$ suy ra $O'$ là trung điểm của $AO$.
Vậy $\triangle AIO \to \triangle AI'O'$ theo đúng thứ tự trên.

a) Ta có $\overrightarrow{IO}=\overrightarrow{v}=\frac{1}{2}\overrightarrow{BC}$.
Theo phép tịnh tiến này thì
$\begin{cases}I \to O \\ A \to M \\O \to N \end{cases}$
Trong đó $M, N$ lần lượt là trung điểm của $AD,DC.$
Như vậy $\triangle AIO \to \triangle MON$ theo đúng thứ tự trên.

c) Ta biết rằng hai mặt phẳng không song song với nhau thì cắt nhau theo một giao tuyến là đường thẳng. Vì thế để xác định đường thẳng này thì ta chỉ cần tìm hai điểm mà đều thuộc cả hai mặt phẳng.
Thứ nhất nếu gọi $A'B$ cắt $AB'$ tại $M$, thì $M$ là trung điểm của hai đoạn thẳng này và suy ra nó đều trên hai mặt phẳng $(AB'C')$ và $(A'BC)$.
Thứ hai nếu gọi $A'C$ cắt $AC'$ tại $N$, thì $N$ là trung điểm của hai đoạn thẳng này và suy ra nó đều trên hai mặt phẳng $(AB'C')$ và $(A'BC)$.
Theo tính chất của đường trung bình thì $MN$ đi qua $O$ xác đinh từ câu b), và giao tuyến cần tìm chính là đường thẳng $MN$.

b) Trong mặt phẳng $A'I'IA$ gọi giao điểm của hai đường thẳng $A'I$ và $AI'$ là $O$ thì $O$ là trung điểm của mỗi đoạn vì đây là hình bình hành.
Điểm $O$ thuộc $AI'$ nên nó cũng nằm trong mặt phẳng $(AB'C')$.
Vì vậy giao điểm của $A'I$ và mặt phẳng $(AB'C')$ chính là điểm $O$.

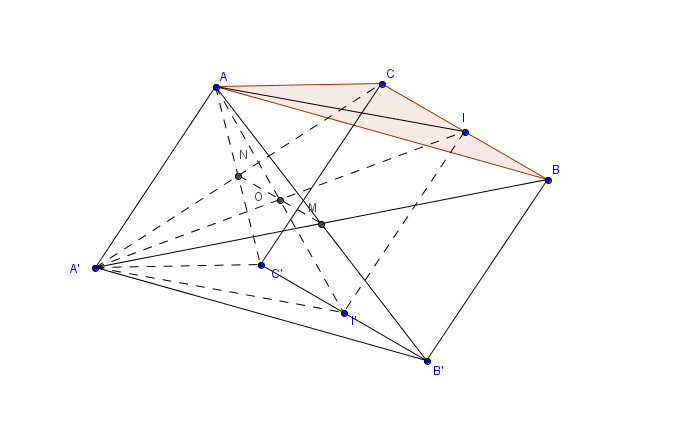a) Do các mặt bên của hình lăng trụ đều là hình bình hành, nói riêng với mặt $BCC'B'$ có $I, I'$ lầ lượt là trung điểm của $BC,B'C;$ nên $II' \parallel BB', II'=BB'.$
Mặt khác cũng có $BB' \parallel AA', BB'=AA'.$
Do đó $II' \parallel AA', II'=AA'.$
Suy ra $AA'I'I$ là hình bình hành và $AI \parallel A'I, AI'=A'I'.$

Điều kiện $\sin 2x \ne 0.$
PT $\Leftrightarrow 2 \cos2x\cos \frac{\pi}{4}-2 \sin2x\sin \frac{\pi}{4}=\frac{\cos x}{\sin x}-\frac{\sin x}{\cos x}-2$
$\Leftrightarrow \sqrt 2\left (  \cos2x-\sin 2x \right )=\frac{\cos^2x-\sin^2 x}{\sin x\cos x}-2$
$\Leftrightarrow \sqrt 2\left (  \cos2x-\sin 2x \right )=\frac{2\cos2x}{\sin 2x}-2$
$\Leftrightarrow \sqrt 2\left (  \cos2x-\sin 2x \right )=\frac{2(\cos2x-\sin 2x)}{\sin 2x}$
$\Leftrightarrow \left[ {\begin{matrix} \cos2x=\sin 2x\\ \sin 2x=\frac{1}{\sqrt 2} \end{matrix}} \right.$
$\Leftrightarrow \left[ {\begin{matrix} \cot2x=1\\ \sin 2x=\frac{1}{\sqrt 2} \end{matrix}} \right.$
$\Leftrightarrow \left[ {\begin{matrix} x=\frac{\pi}{8}+k\frac{\pi}{2}\\ x=\frac{\pi}{8}+k\pi\\x=\frac{3\pi}{8}+k\pi \\\end{matrix}} \right.     (k \in \mathbb{Z}).$