|
|
giải đáp
|
gpt
|
|
|
|
PT $\Leftrightarrow 2\sin x \cos x -3(1-\cos x)=0\Leftrightarrow 4\sin \frac{x}{2}\cos \frac{x}{2}\cos x-6\sin^2\frac{x}{2}=0$ Nếu $\sin \frac{x}{2}=0\Leftrightarrow x=k2\pi/$ Nếu $\sin \frac{x}{2} \ne 0 \Rightarrow 2\cos \frac{x}{2}\cos x=3\sin\frac{x}{2}\Rightarrow 2\cos x=3\tan \frac{x}{2}$ Đặt $t=\tan \frac{x}{2}$ thì PT trên trở thành $\frac{2(1-t^2)}{1+t^2}=3t\Leftrightarrow 3t^3+2t^2+3t-2=0$ Đây là pt bậc ba có nghiệm duy nhất nhưng không đẹp, có thể giải bằng pp Cardano $t$ 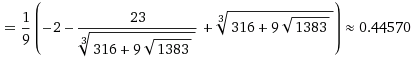 |
|
|
|
sửa đổi
|
Một bạn trên facebook hỏi
|
|
|
|
Gọi $O$ là tâm hình vuông.Ta có:$Q(O,90^\circ): B\rightarrow A, A\rightarrow D,$do đó, qua phép quay này, đường thẳng $BA$ biến thành đường thẳng $AD$ và $M \in AB \rightarrow M'\in AD, N\rightarrow N'$.Ta cũng có: $Q(O,90^\circ): C\rightarrow B; D\rightarrow C,$do đó, qua phép quay này, đường thẳng $CD$ biến thành đường thẳng $BC$ và $N\rightarrow N'$. Theo tính chất của phép quay ta có$MN=M'N'$ và $MN \bot M'N'$Theo
giả thiết $MN\bot PQ$ vì vậy hoặc $PQ \parallel M'N'$ hoặc $PQ \equiv
M'N'$. Trong cả hai trường hợp, ta đều suy ra được $MN=PQ$.
Gọi $O$ là tâm hình vuông.Ta có:$Q(O,90^\circ): B\rightarrow A, A\rightarrow D,$do đó, qua phép quay này, đường thẳng $BA$ biến thành đường thẳng $AD$ và $M \in AB \rightarrow M'\in AD, N\rightarrow N'$.Ta cũng có: $Q(O,90^\circ): C\rightarrow B; D\rightarrow C,$do đó, qua phép quay này, đường thẳng $CD$ biến thành đường thẳng $BC$ và $N\rightarrow N'$. Theo tính chất của phép quay ta có$MN=M'N'$ và $MN \bot M'N'$Theo
giả thiết $MN\bot PQ$ vì vậy hoặc $PQ \parallel M'N'$ hoặc $PQ \equiv
M'N'$. Trong cả hai trường hợp, ta đều suy ra được $MN=PQ$.
|
|
|
|
sửa đổi
|
phép biến hình lớp 11
|
|
|
|
phép biến hình lớp 11 cho hình vuông ABCD đường thẳng d cắt AB và CD tương ứng tại M và N. Đường thẳng d' vuông góc với d cắt AD và BC tại P và Q. Chứng minh : MN=PQ
phép biến hình lớp 11 Cho hình vuông $ABCD $.Một đường thẳng $d $ cắt các đường thẳng $AB $ và $CD $ tương ứng tại các điểm $M , N $. Một đường thẳng $d' $ vuông góc với $d $ cắt các đường thẳng $AD $ và $BC $ tương ứng tại các điểm $P $ và $Q $. Chứng minh rằng $MN=PQ $.
|
|
|
|
bình luận
|
phép biến hình lớp 11
Hãy ấn chữ V dưới đáp án để chấp nhận nếu như bạn thấy lời giải này chính xác, và nút mũi tên màu xanh để vote up nhé. Thanks!
|
|
|
|
|
|
|
|
giải đáp
|
phép biến hình lớp 11
|
|
|
|
 Gọi $O$ là tâm hình vuông. Ta có:$Q(O,90^\circ): B\rightarrow A, A\rightarrow D,$ do đó, qua phép quay này, đường thẳng $BA$ biến thành đường thẳng $AD$ và $M \in AB \rightarrow M'\in AD, N\rightarrow N'$. Ta cũng có: $Q(O,90^\circ): C\rightarrow B; D\rightarrow C,$ do đó, qua phép quay này, đường thẳng $CD$ biến thành đường thẳng $BC$ và $N\rightarrow N'$. Theo tính chất của phép quay ta có $MN=M'N'$ và $MN \bot M'N'$ Theo giả thiết $MN\bot PQ$ vì vậy hoặc $PQ \parallel M'N'$ hoặc $PQ \equiv M'N'$. Trong cả hai trường hợp, ta đều suy ra được $MN=PQ$. |
|
|
|
giải đáp
|
Một bạn trên facebook hỏi
|
|
|
|
 Gọi $O$ là tâm hình vuông. Ta có:$Q(O,90^\circ): B\rightarrow A, A\rightarrow D,$ do đó, qua phép quay này, đường thẳng $BA$ biến thành đường thẳng $AD$ và $M \in AB \rightarrow M'\in AD, N\rightarrow N'$. Ta cũng có: $Q(O,90^\circ): C\rightarrow B; D\rightarrow C,$ do đó, qua phép quay này, đường thẳng $CD$ biến thành đường thẳng $BC$ và $N\rightarrow N'$. Theo tính chất của phép quay ta có $MN=M'N'$ và $MN \bot M'N'$ Theo
giả thiết $MN\bot PQ$ vì vậy hoặc $PQ \parallel M'N'$ hoặc $PQ \equiv
M'N'$. Trong cả hai trường hợp, ta đều suy ra được $MN=PQ$. |
|
|
|
bình luận
|
TOÁN 11
Hãy ấn chữ V dưới đáp án để chấp nhận nếu như bạn thấy lời giải này chính xác, và nút mũi tên màu xanh để vote up nhé. Thanks!
|
|
|
|
|
|
|
|
giải đáp
|
TOÁN 11
|
|
|
|
a) Xét phép quay $Q_A$ tâm $A$ góc quay $90^\circ$ chiều dương là chiều ngược chiều kim đồng hồ.
$Q_A : N \to B, C \to Q$
suy ra $CN=BQ, CN \perp BQ.$
|
|
|
|
bình luận
|
Phương trình lượng giác.
Hãy ấn chữ V dưới đáp án để chấp nhận nếu như bạn thấy lời giải này chính xác, và nút mũi tên màu xanh để vote up nhé. Thanks!
|
|
|
|
|
|
|
|
giải đáp
|
Phương trình lượng giác.
|
|
|
|
PT $\Leftrightarrow \cos 3x=\sin 5x \Leftrightarrow \cos 3x= \cos \left ( \frac{\pi}{2} -5x\right )$
$\Leftrightarrow \left[ {\begin{matrix} 3x= \frac{\pi}{2} -5x+k2\pi\\ 3x=- \frac{\pi}{2} +5x+k2\pi \end{matrix}} \right.$
$\Leftrightarrow \left[ {\begin{matrix} x= \frac{\pi}{16}+k\frac{\pi}{4}\\ x= \frac{\pi}{4} -k\pi \end{matrix}} \right. (k \in \mathbb{Z}).$
|
|
|
|
bình luận
|
Nhị thức Newton
Hãy ấn chữ V dưới đáp án để chấp nhận nếu như bạn thấy lời giải này chính xác, và nút mũi tên màu xanh để vote up nhé. Thanks!
|
|
|
|
|
|
|
|
giải đáp
|
Nhị thức Newton
|
|
|
|
Trước hết bạn chứng minh công thức sau coi như bài tập nhé
$C_n^k+C_n^{k+1}=C_{n+1}^{k+1}$
Áp dụng công thức này ta có
$S=\left (C_{29}^{13}+C_{29}^{14} \right )-\left (C_{29}^{14}+C_{29}^{15} \right )+\left (C_{29}^{15}+C_{29}^{16} \right )-\cdots+\left (C_{29}^{27}+C_{29}^{28} \right )-\left (C_{29}^{28}+C_{29}^{29} \right )+C_{29}^{29}$
$S=C_{29}^{13}$
|
|
|
|
|
|
|
|
sửa đổi
|
Chứng minh đẳng thức lượng giác trong tam giác
|
|
|
|
cho tam giác ABCCh o tam gi ác ABC: CMR : $(a-b)cot\frac{C}{2} + (b-c)cot\frac{A}{2} + (c-a)cot\frac{B}{2} = 0 $ thx mọi người
Ch ứng minh đẳng thức lượng giác tro ng tam giác Ch ứng mi nh rằng: $(a-b) \cot \frac{ C}{2 } +(b-c) \cot \frac{ A}{ 2} +(c-a) \cot \frac{ B}{ 2} =0 (1)$
|
|