|
|
bình luận
|
Tọa độ điểm.
Hãy ấn chữ V dưới đáp án để chấp nhận nếu như bạn thấy lời giải này chính xác, và nút mũi tên màu xanh để vote up nhé. Thanks!
|
|
|
|
|
|
|
|
giải đáp
|
Tọa độ điểm.
|
|
|
|
Gọi $M(a, b) \in (E)$ thì ta có $a^2+4b^2=8$.
Ta cần tìm GTNN của $MA^2=(a-4)^2+(b-5)^2$.
Ta có
$(a-4)^2+(b-5)^2=a^2-8a+b^2-10+41=2a^2-8a+8+5b^2-10b+5+28-(a^2+4b^2)$
$=2(a-2)^2+5(b-1)^2+20$, do $a^2+4b^2=8$.
Suy ra $MA^2 \ge 20 \Leftrightarrow MA \ge 2\sqrt 5$.
Vậy $\min MA=2\sqrt 5\Leftrightarrow a=2,b=1\Leftrightarrow M(2;1).$
|
|
|
|
bình luận
|
hỏi bài này với nhé
Hãy ấn chữ V dưới đáp án để chấp nhận nếu như bạn thấy lời giải này chính xác, và nút mũi tên màu xanh để vote up nhé. Thanks!
|
|
|
|
|
|
|
|
giải đáp
|
hỏi bài này với nhé
|
|
|
|
Nhận thấy rằng $x^2-3x+4 = (x-\frac{3}{2})^2+\frac{7}{4}> 0 \forall x.$
Do đó BPT $\Leftrightarrow x^2-kx-2>-x^2+3x-4\Leftrightarrow 2x^2-(k+3)x+2>0$.
Đây là BPT bậc hai ẩn $x$ tham số $k$ có hệ số $a=2>0$, nên để BPT này nghiệm đúng với mọi $x$ thì cần điều kiện
$\Delta<0\Leftrightarrow (k+3)^2-16<0\Leftrightarrow -4<k+3<4\Leftrightarrow \boxed{-7<k<1}$.
|
|
|
|
bình luận
|
đố mọi người nha
Hãy ấn chữ V dưới đáp án để chấp nhận nếu như bạn thấy lời giải này chính xác, và nút mũi tên màu xanh để vote up nhé. Thanks!
|
|
|
|
|
|
|
|
giải đáp
|
đố mọi người nha
|
|
|
|
b) Tập hợp các điểm $M(x,y)$ thỏa mãn bài toán là tập hợp các điểm có cả hai tọa độ đều nguyên, $x, y \in \mathbb{Z}$ và nằm trong phần mặt phẳng được kẻ ngang như trong hình vẽ câu a.
|
|
|
|
bình luận
|
đố mọi người nha
Hãy ấn chữ V dưới đáp án để chấp nhận nếu như bạn thấy lời giải này chính xác, và nút mũi tên màu xanh để vote up nhé. Thanks!
|
|
|
|
|
|
|
|
giải đáp
|
đố mọi người nha
|
|
|
|
a) Viết lại BPT dưới dạng $y \le 4-\frac{4}{3}x$. Nhận thấy rằng gốc tọa độ $O(0,0)$ thỏa mãn PT này nên tập hợp các điểm biểu diễn là nửa mặt phẳng chứa điểm $O$ và có bờ là đường thằng $y=4-\frac{4}{3}x$ như hình vẽ. 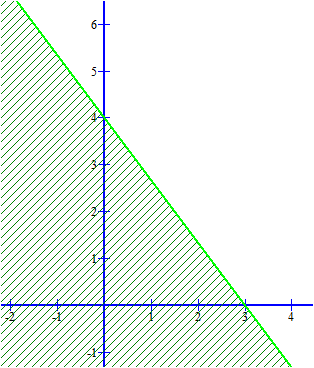 |
|
|
|
|
|
sửa đổi
|
bài này nữa ah
|
|
|
|
bài này nữa ah Giải các bất phương trình :$\begin{array}{l}1)\,\,\,\,\,{\left( {\frac{1}{2}} \right)^{\log _{\frac{1}{2}}^2x}} \le {x^3}\\2)\,\,\,\,{5^{{{\log }_{\frac{1}{2}}}{{\log }_2}\displaystyle\left( {{3^{2{{\log }_3}x - 3 + {{\log }_3}9}}} \right)}} < 1\end{array}$
bài này nữa ah Giải các bất phương trình :$\begin{array}{l}1)\,\,\,\,\,{\left( {\frac{1}{2}} \right)^{\log _{\frac{1}{2}}^2x}} \le {x^3}\\2)\,\,\,\,{5^{{{\log }_{\frac{1}{2}}}{{\log }_2}\displaystyle\left( {{3^{2{{\log }_3}x - 3 x + {{\log }_3}9}}} \right)}} < 1\end{array}$
|
|
|
|
bình luận
|
Giải các bất phương trình :
Hãy ấn chữ V dưới đáp án để chấp nhận nếu như bạn thấy lời giải này chính xác, và nút mũi tên màu xanh để vote up nhé. Thanks!
|
|
|
|
|
|
|
|
sửa đổi
|
bài này nữa ah
|
|
|
|
2)PT $\Leftrightarrow {{\log }_{\frac{1}{2}}}{{\log }_2}\left( {{3^{2{{\log }_3}x - 3 + {{\log }_3}9}}} \right)<0\Leftrightarrow {{\log }_2}\left( {{3^{2{{\log }_3}x - 3 + {{\log }_3}9}}} \right)>1$$\Leftrightarrow 3^{2{{\log }_3}x - 3 + {{\log }_3}9}>2\Leftrightarrow 2{{\log }_3}x - 3 + {{\log }_3}9>\log_32$$\Leftrightarrow 2{{\log }_3}x >\log_32+1\Leftrightarrow x^2>6\Leftrightarrow x > \sqrt 6$
2)PT $\Leftrightarrow {{\log }_{\frac{1}{2}}}{{\log }_2}\left(
{{3^{2{{\log }_3}x - 3x + {{\log }_3}9}}} \right)<0\Leftrightarrow
{{\log }_2}\left( {{3^{2{{\log }_3}x - 3x + {{\log }_3}9}}} \right)>1$$\Leftrightarrow 3^{2{{\log }_3}x - 3x + {{\log }_3}9}>2\Leftrightarrow 2{{\log }_3}x - 3x + {{\log }_3}9>\log_32$$\Leftrightarrow 2{{\log }_3}x -3x+2-\log_32>0$Xét hàm số $f(x)= 2{{\log }_3}x -3x+2-\log_32$có $f'(x)=\frac{2}{x \ln 3}-3=0\Leftrightarrow x=\frac{2}{3 \ln 3}$Lập bảng biến thiên của $f(x)$ ta thấy rằng $f(x) \le f(\frac{2}{3 \ln 3})<0$.Vì thế BPT đã cho vô nghiệm.
|
|
|
|
giải đáp
|
Giải các bất phương trình :
|
|
|
|
2)
PT $\Leftrightarrow {{\log }_{\frac{1}{2}}}{{\log }_2}\left(
{{3^{2{{\log }_3}x - 3x + {{\log }_3}9}}} \right)<0\Leftrightarrow
{{\log }_2}\left( {{3^{2{{\log }_3}x - 3x + {{\log }_3}9}}} \right)>1$
$\Leftrightarrow 3^{2{{\log }_3}x - 3x + {{\log }_3}9}>2\Leftrightarrow 2{{\log }_3}x - 3x + {{\log }_3}9>\log_32$
$\Leftrightarrow 2{{\log }_3}x -3x+2-\log_32>0$
Xét hàm số $f(x)= 2{{\log }_3}x -3x+2-\log_32$
có $f'(x)=\frac{2}{x \ln 3}-3=0\Leftrightarrow x=\frac{2}{3 \ln 3}$
Lập bảng biến thiên của $f(x)$ ta thấy rằng $f(x) \le f(\frac{2}{3 \ln 3})<0$.
Vì thế BPT đã cho vô nghiệm.
|
|
|
|
bình luận
|
Giải bất phương trình :
Hãy ấn chữ V dưới đáp án để chấp nhận nếu như bạn thấy lời giải này chính xác, và nút mũi tên màu xanh để vote up nhé. Thanks!
|
|
|
|
|
|
|
|
bình luận
|
Giải bất phương trình :
Hãy ấn chữ V dưới đáp án để chấp nhận nếu như bạn thấy lời giải này chính xác, và nút mũi tên màu xanh để vote up nhé. Thanks!
|
|
|
|
|
|