b)


Vậy Kết Quả là $C_5^3.C_5^3.6!-C_5^3.C_4^2.5!=64800$ số.

a)

b)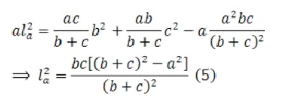

Điều này có nghĩa là
$AD=l_a=\frac{2}{b+c}\sqrt{bcp(p-a)}$ (đpcm)

a)

3) Điều kiện $x >0$. Do $1/2<1$ nên ta có
BPT $\Leftrightarrow 3{\log _{\frac{1}{2}}}x < 1\Leftrightarrow {\log _{\frac{1}{2}}}x < 1/3\Leftrightarrow x>(1/2)^{1/3}=\frac{1}{\sqrt[3]{2}}$

h) Điều kiện: $x^2-3x+2>0\Leftrightarrow \left[ \begin{array}{l} x>2\\x<1 \end{array} \right.$
Phương trình tương đương với:
$\displaystyle\frac{1}{2}\log_3(x^2-3x+2)+\left(\frac{1}{5}\right)^{3x-x^2-1}=2$
Đặt: $x^2-3x+2=t$, phương trình trở thành:
$\displaystyle\frac{1}{2}\log_3t+\left(\frac{1}{5}\right)^{1-t}=2$
Xét hàm: $\displaystyle f(t)=\frac{1}{2}\log_3t+\left(\frac{1}{5}\right)^{1-t},t>0$
Ta có: $\displaystyle f'(t)=\frac{1}{2t\ln3}-\left(\frac{1}{5}\right)^{1-t}\ln\left(\frac{1}{5}\right)>0,\forall t>0$
Suy ra $f(t)=2$ có nhiều nhất 1 nghiệm.
Mà $f(t)=2$ có nghiệm rất xấu. $t\approx 1,383045303$

g) Ta có:
$\log_5(5^x+1).\log_{25}(5^{x+1}+5)=2m+1$
$\Leftrightarrow \log_5(5^x+1).\frac{1}{2}(\log_5(5^x+1)+1)=2m+1$ 
Đặt $t=\log_5(5^x+1)$ thì suy ra $t>0$.
Phương trình trở thành: $t(t+1)=2(2m+1)$ 
                   $\Leftrightarrow m=\frac{t^2+t-2}{4}$ 
Xét hàm: $f(t)=  \frac{t^2+t-2}{4}$ với $t>0$
ta có: $f'(t)=\frac{2t+1}{4}>0,\forall t>0$ 
Suy ra: $m>f(0)=\frac{-1}{2}$ 
Vậy phương trình đã cho có nghiệm với: $m>\frac{-1}{2}$