|
|
giải đáp
|
Tích phân
|
|
|
|
c)
$K = \int\limits_{0}^{1} (1+3x)(1+2x+3x^2)^{10} dx=\frac{1}{2} \int\limits_{0}^{1} (1+2x+3x^2)^{10} d(1+2x+3x^2)$
$=\frac{1}{2}\left[ {\frac{(1+2x+3x^2)^{11}}{11}} \right]_0^1=\frac{1}{2}\left ( \frac{6^{11}-1}{11} \right )$
|
|
|
|
giải đáp
|
BPT mũ có Lượng giác
|
|
|
|
a) Với $m=1$ thì BPT $\Leftrightarrow 2^{2\tan x}+ 2^{\tan x}-2 \le 0\Leftrightarrow ( 2^{\tan x}+2)( 2^{\tan x}-1) \le 0$
$\Leftrightarrow2^{\tan x}-1 \le 0\Leftrightarrow 2^{\tan x}\le1\Leftrightarrow \tan x \le 0\Leftrightarrow x \in (-\pi/2+k\pi;k\pi] \cup(\pi/2+l\pi; \pi+l\pi]$
|
|
|
|
giải đáp
|
Tích phân
|
|
|
|
a)
$ I = \int\limits_{0}^{1} \frac{e^x}{1+e^x}dx= I = \int\limits_{0}^{1} \frac{d(1+e^x)}{1+e^x}=\left[ {\ln (e^x+1)} \right]_0^1=\ln(e+1)-\ln2$
|
|
|
|
bình luận
|
Bất phương trình Lôgarit
Hãy ấn chữ V dưới đáp án để chấp nhận nếu như bạn thấy lời giải này chính xác, và nút mũi tên màu xanh để vote up nhé. Thanks!
|
|
|
|
|
|
|
|
|
|
bình luận
|
Bất phương trình Lôgarit
Hãy ấn chữ V dưới đáp án để chấp nhận nếu như bạn thấy lời giải này chính xác, và nút mũi tên màu xanh để vote up nhé. Thanks!
|
|
|
|
|
|
|
|
|
|
bình luận
|
Giúp em nhé
Hãy ấn chữ V dưới đáp án để chấp nhận nếu như bạn thấy lời giải này chính xác, và nút mũi tên màu xanh để vote up nhé. Thanks!
|
|
|
|
|
|
|
|
giải đáp
|
Giúp em nhé
|
|
|
|
a) Áp dụng BĐT tam giác ta có
$\begin{cases}\frac{2}{3}m_a+\frac{2}{3}m_b >c \\ \frac{2}{3}m_a+\frac{2}{3}m_c >b \\ \frac{2}{3}m_b+\frac{2}{3}m_c >a \end{cases}\Rightarrow \frac{3}{4} (a+b+c)<m_a+m_b+m_c$
Vẽ thêm điểm D để tạo ra hình bình hành ABCD và áp dụng BĐT tam giác ta có $2m_a<b+c$
$\Rightarrow \begin{cases}2m_a<b+c \\ 2m_b<a+c \\ 2m_c<b+a \\ \end{cases}\Rightarrow m_a+m_b+m_c<a+b+c$
|
|
|
|
giải đáp
|
Phương trình vô tỉ.
|
|
|
|
3. Điều kiện $x \ge -2$
$x^2+2x-2\sqrt{x+2}=4\Leftrightarrow x^2+2x-8-2(\sqrt{x+2}-2)=0$
$\Leftrightarrow (x+4)(x-2)-2(x-2)\frac{2}{\sqrt{x+2}+2}=0$
Do $x+4 \ge 2 >1\ge \frac{2}{\sqrt{x+2}+2}$.
Do vậy PT $\Leftrightarrow x=2.$
|
|
|
|
|
|
bình luận
|
Giúp em nhé
Hãy ấn chữ V dưới đáp án để chấp nhận nếu như bạn thấy lời giải này chính xác, và nút mũi tên màu xanh để vote up nhé. Thanks!
|
|
|
|
|
|
|
|
|
|
sửa đổi
|
Một bạn trên facebook hỏi
|
|
|
|
Áp dụng Định lý Py-ta-go ta được$MB^2-MC^2=(KB^2+KM^2)-(KC^2+KM^2)=KB^2-KC^2=(KB-KC)(KB+KC)$$=(KB-KH)(KB+KC)=BH.BC=AB^2=\boxed{16 cm^2.}$
Áp dụng Định lý Py-ta-go ta được$MB^2-MC^2=(KB^2+KM^2)-(KC^2+KM^2)=KB^2-KC^2=(KB-KC)(KB+KC)$$=(KB-KH)(KB+KC)=BH.BC=AB^2=\boxed{16 cm^2.}$
|
|
|
|
giải đáp
|
Một bạn trên facebook hỏi
|
|
|
|
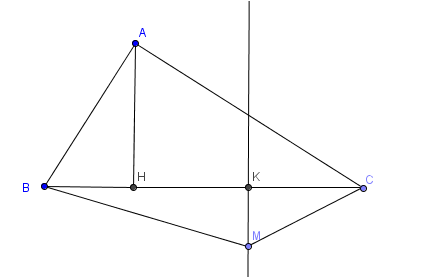 Áp dụng Định lý Py-ta-go ta được $MB^2-MC^2=(KB^2+KM^2)-(KC^2+KM^2)=KB^2-KC^2=(KB-KC)(KB+KC)$ $=(KB-KH)(KB+KC)=BH.BC=AB^2=\boxed{16 cm^2.}$ |
|