|
|
bình luận
|
giải giúp c nhanh nha.
Bạn xem lại đi nhé. Đây là mình sửa lại thành câu c) Còn câu a) bạn khangnguyenthanh làm đúng rồi
|
|
|
|
|
|
|
|
sửa đổi
|
giải giúp c nhanh nha.
|
|
|
|
a) PT có nghiệm dương $\Leftrightarrow \begin{cases}\Delta' \ge 0 \\ S=-\frac{b}{a}>0 \\ P=\frac{c}{a}>0\end{cases}\Leftrightarrow \begin{cases}m(m+3) \ge 0 \\ 2(m+1)>0 \\ 1-m>0\end{cases} \Leftrightarrow 1>m \ge 0$
c) PT có hai nghiệm đều âm$\Leftrightarrow \begin{cases}m \ne 0\\\Delta' \ge 0 \\ S=-\frac{b}{a}<0 \\ P=\frac{c}{a}>0\end{cases}\Leftrightarrow \begin{cases}m\ne 0 \\12m+1 \ge 0 \\ -\frac{2m+1}{m}<0 \\ \frac{m-2}{m}>0\end{cases} \Leftrightarrow m>2$
|
|
|
|
bình luận
|
giải giúp c nhanh nha.
Hãy ấn chữ V dưới đáp án để chấp nhận nếu như bạn thấy lời giải này chính xác, và nút mũi tên màu xanh để vote up nhé. Thanks!
|
|
|
|
|
|
|
|
giải đáp
|
giải giúp c nhanh nha.
|
|
|
|
b) $x^2-2x(m-2)=0\Leftrightarrow x(x-2m+4)=0\Leftrightarrow \left[ {\begin{matrix} x=0\\ x=2(m-2) \end{matrix}} \right.$
Nhận thấy với mọi giá trị của $m$ thì PT đều có nghiệm $x=0$, không âm.
Nếu câu hỏi được thay đổi là tìm $m$ để PT có nghiệm dương thì điều kiện là $m>2.$
|
|
|
|
bình luận
|
giải giúp c nhanh nha.
Hãy ấn chữ V dưới đáp án để chấp nhận nếu như bạn thấy lời giải này chính xác, và nút mũi tên màu xanh để vote up nhé. Thanks!
|
|
|
|
|
|
|
|
giải đáp
|
giải giúp c nhanh nha.
|
|
|
|
c) PT có hai nghiệm đều âm
$\Leftrightarrow \begin{cases}m \ne 0\\\Delta' \ge 0 \\ S=-\frac{b}{a}<0 \\ P=\frac{c}{a}>0\end{cases}\Leftrightarrow \begin{cases}m\ne 0 \\12m+1 \ge 0 \\ -\frac{2m+1}{m}<0 \\ \frac{m-2}{m}>0\end{cases} \Leftrightarrow m>2$
|
|
|
|
bình luận
|
Chứng minh trung điểm
Hãy ấn chữ V dưới đáp án để chấp nhận nếu như bạn thấy lời giải này chính xác, và nút mũi tên màu xanh để vote up nhé. Thanks!
|
|
|
|
|
|
|
|
sửa đổi
|
Chứng minh trung điểm
|
|
|
|
Các điểm được ký hiệu như trên hình vẽ. Và ta cần chứng minh giao điểm $M, N$ là các trung điểm của $AB,DC$.Thật vậy theo định lý Talet$\frac{AM}{DN}=\frac{SA}{SA}=\frac{AB}{CD}=\frac{AO}{CO}=\frac{AM}{CN}$Tóm lại $\frac{AM}{DN}=\frac{AM}{CN} \implies DN=CN$ hay $N$ là trung điểm $CD$.CHứng minh tương tự ta cũng có $M$ là trung điểm $AB$.
Các điểm được ký hiệu như trên hình vẽ. Và ta cần chứng minh giao điểm $M, N$ là các trung điểm của $AB,DC$.Thật vậy theo định lý Talet$\frac{AM}{DN}=\frac{SA}{SA}=\frac{AB}{CD}=\frac{AO}{CO}=\frac{AM}{CN}$Tóm lại $\frac{AM}{DN}=\frac{AM}{CN} \implies DN=CN$ hay $N$ là trung điểm $CD$.CHứng minh tương tự ta cũng có $M$ là trung điểm $AB$.
|
|
|
|
giải đáp
|
Chứng minh trung điểm
|
|
|
|
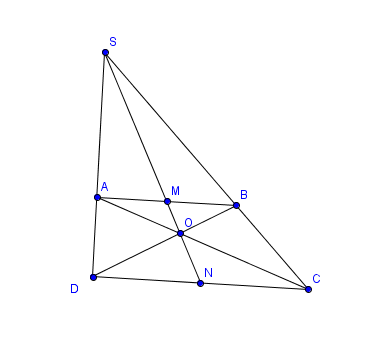 Các điểm được ký hiệu như trên hình vẽ. Và ta cần chứng minh giao điểm $M, N$ là các trung điểm của $AB,DC$. Thật vậy theo định lý Talet $\frac{AM}{DN}=\frac{SA}{SD}=\frac{AB}{CD}=\frac{AO}{CO}=\frac{AM}{CN}$ Tóm lại $\frac{AM}{DN}=\frac{AM}{CN} \implies DN=CN$ hay $N$ là trung điểm $CD$. CHứng minh tương tự ta cũng có $M$ là trung điểm $AB$. |
|
|
|
|
|
giải đáp
|
Em tìm trong thư viện nhưng ko có lời giải
|
|
|
|
b) Thấy rằng $\sin\frac{\pi}{n} \ne 0$ và áp dụng công thức $2\sin a \sin b= \cos (a-b) -\cos (a+b)$
$\sum\limits_{i=1}^n 2\sin \frac{2(i-1)\pi}{n}\sin\frac{\pi}{n}=\sum\limits_{i=1}^n\left ( \cos \frac{(2i-3)\pi}{n}-\cos \frac{(2i-1)\pi}{n}\right )=$
$ \cos \frac{-\pi}{n}-\cos \frac{(2n-1)\pi}{n} =\cos \frac{\pi}{n}- \cos \left ( 2\pi- \frac{\pi}{n}\right )=0$
Từ đây suy ra đpcm.
|
|
|
|
|
|
giải đáp
|
Em tìm trong thư viện nhưng ko có lời giải
|
|
|
|
a) Thấy rằng $\sin\frac{\pi}{n} \ne 0$ và áp dụng công thức $2\cos a \sin b= \sin (a+b) -\sin (a-b)$
$\sum\limits_{i=1}^n 2\cos \frac{2(i-1)\pi}{n}\sin\frac{\pi}{n}=\sum\limits_{i=1}^n\left ( \sin \frac{(2i-1)\pi}{n}-\sin \frac{(2i-3)\pi}{n}\right )=$
$ \sin \frac{(2n-1)\pi}{n}+ \sin \frac{\pi}{n}= \sin \left ( 2\pi- \frac{\pi}{n}\right )+ \sin \frac{\pi}{n}=0$
Từ đây suy ra đpcm.
|
|
|
|
bình luận
|
đố mọi người bài này nhé
Hãy ấn chữ V dưới đáp án để chấp nhận nếu như bạn thấy lời giải này chính xác, và nút mũi tên màu xanh để vote up nhé. Thanks!
|
|
|
|
|
|
|
|
bình luận
|
đố mọi người bài này nhé
Hãy ấn chữ V dưới đáp án để chấp nhận nếu như bạn thấy lời giải này chính xác, và nút mũi tên màu xanh để vote up nhé. Thanks!
|
|
|
|
|
|